
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
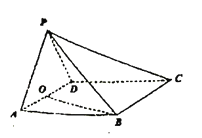
(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)證明見解析;(2) ![]()
【解析】
(1)求出![]() 和
和![]() 的數量關系,根據勾股定理可證
的數量關系,根據勾股定理可證![]() ,又
,又![]() 是正三角形,所以
是正三角形,所以![]() ,根據直線與平面垂直的判定定理,可證
,根據直線與平面垂直的判定定理,可證![]() 平面
平面![]() ;
;
(2)建立空間直角坐標系,求出兩平面的法向量所成的余弦值,從而可以求出平面![]() 與平面
與平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
(1)證明:連結![]() ,
,![]() ,因為底面
,因為底面![]() 為菱形,
為菱形,![]() ,
,
故![]() ,又
,又![]() 為
為![]() 的中點,故
的中點,故![]() .
.
在![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,所以
的中點,所以![]() .
.
設![]() ,則
,則![]() ,
,![]() ,
,
因為![]() ,
,
所以![]() .(也可通過
.(也可通過![]() 來證明
來證明![]() ),
),
又因為![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)因為![]() ,
,![]() ,
,
![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
由(1)得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,故有
,故有![]() ,又由
,又由![]() ,
,
所以![]() ,
,![]() ,
,![]() 所在的直線兩兩互相垂直.
所在的直線兩兩互相垂直.
故以![]() 為坐標原點,以
為坐標原點,以![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸如圖建系.
軸如圖建系.
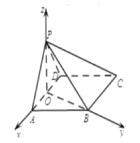
設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 平面
平面![]() ,
,
故可以取與![]() 平行的向量
平行的向量![]() 作為平面
作為平面![]() 的法向量.
的法向量.
設平面![]() 的法向量為
的法向量為![]() ,則
,則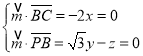 ,
,
令![]() ,所以
,所以![]() .
.
設平面![]() 與平面
與平面![]() 所成二面角為
所成二面角為![]() ,而
,而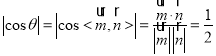
則![]() ,所以平面
,所以平面![]() 與平面
與平面![]() 所成二面角的正弦值為
所成二面角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
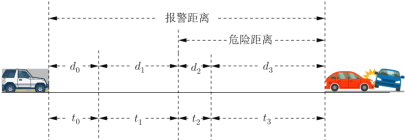
【題目】汽車智能輔助駕駛已得到廣泛應用,其自動剎車的工作原理是用雷達測出車輛與前方障礙物之間的距離(并結合車速轉化為所需時間),當此距離等于報警距離時就開始報警提醒,等于危險距離時就自動剎車,某種算法(如下圖所示)將報警時間劃分為4段,分別為準備時間![]() 、人的反應時間
、人的反應時間![]() 、系統反應時間
、系統反應時間![]() 、制動時間
、制動時間![]() ,相應的距離分別為
,相應的距離分別為![]() 、
、![]() 、
、![]() 、
、![]() ,當車速為
,當車速為![]() (米/秒),且
(米/秒),且![]() 時,通過大數據統計分析得到下表(其中系數
時,通過大數據統計分析得到下表(其中系數![]() 隨地面濕滑成都等路面情況而變化,
隨地面濕滑成都等路面情況而變化,![]() ).
).
階段 | 0、準備 | 1、人的反應 | 2、系統反應 | 3、制動 |
時間 |
|
|
|
|
距離 |
|
|
|
|
(1)請寫出報警距離![]() (米)與車速
(米)與車速![]() (米/秒)之間的函數關系式
(米/秒)之間的函數關系式![]() ,并求
,并求![]() 時,若汽車達到報警距離時人和系統均不采取任何制動措施,仍以此速度行駛,則汽車撞上固定障礙物的最短時間(精確到0.1秒);
時,若汽車達到報警距離時人和系統均不采取任何制動措施,仍以此速度行駛,則汽車撞上固定障礙物的最短時間(精確到0.1秒);
(2)若要求汽車不論在何種路面情況下行駛,報警距離均小于80米,則汽車的行駛速度應限制在多少米/秒以下?合多少千米/小時?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度得到
個單位長度得到![]() 的圖象,若
的圖象,若![]() 的對稱中心為坐標原點,則關于函數
的對稱中心為坐標原點,則關于函數![]() 有下述四個結論:
有下述四個結論:
①![]() 的最小正周期為
的最小正周期為![]() ②若
②若![]() 的最大值為2,則
的最大值為2,則![]()
③![]() 在
在![]() 有兩個零點 ④
有兩個零點 ④![]() 在區間
在區間![]() 上單調
上單調
其中所有正確結論的標號是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系.若曲線
軸正半軸為極軸建立極坐標系.若曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,![]() 點的極坐標為
點的極坐標為![]() ,在平面直角坐標系中,直線
,在平面直角坐標系中,直線![]() 經過點
經過點![]() ,且傾斜角為
,且傾斜角為![]() .
.
(1)寫出曲線![]() 的直角坐標方程以及點
的直角坐標方程以及點![]() 的直角坐標;
的直角坐標;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 參數方程為
參數方程為![]() 為參數),將曲線
為參數),將曲線![]() 上所有點的橫坐標變為原來的
上所有點的橫坐標變為原來的![]() ,縱坐標變為原來的
,縱坐標變為原來的![]() ,得到曲線
,得到曲線![]() .
.
(1)求曲線![]() 的普通方程;
的普通方程;
(2)過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 取得最小值時
取得最小值時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省新課改后某校為預測2020屆高三畢業班的本科上線情況,從該校上一屆高三(1)班到高三(5)班隨機抽取50人,得到各班抽取的人數和其中本科上線人數,并將抽取數據制成下面的條形統計圖.
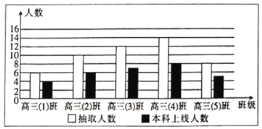
(1)根據條形統計圖,估計本屆高三學生本科上線率.
(2)已知該省甲市2020屆高考考生人數為4萬,假設以(1)中的本科上線率作為甲市每個考生本科上線的概率.
(i)若從甲市隨機抽取10名高三學生,求恰有8名學生達到本科線的概率(結果精確到0.01);
(ii)已知該省乙市2020屆高考考生人數為3.6萬,假設該市每個考生本科上線率均為![]() ,若2020屆高考本科上線人數乙市的均值不低于甲市,求p的取值范圍.
,若2020屆高考本科上線人數乙市的均值不低于甲市,求p的取值范圍.
可能用到的參考數據:取![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com