
在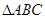 中,角
中,角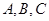 的對邊分別為
的對邊分別為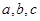 ,且
,且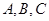 成等差數(shù)列
成等差數(shù)列
(1)若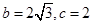 ,求
,求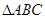 的面積
的面積
(2)若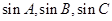 成等比數(shù)列,試判斷
成等比數(shù)列,試判斷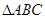 的形狀
的形狀
(1)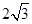 (2)等邊三角形.
(2)等邊三角形.
解析試題分析:(1)根據(jù)A、B、C成等差數(shù)列,結(jié)合A+B+C=π算出B= ,再由正弦定理得:
,再由正弦定理得: .根據(jù)b>c得C為銳角,得到C=
.根據(jù)b>c得C為銳角,得到C=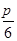 ,從而A=π-B-C=
,從而A=π-B-C=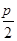 ,△ABC是直角三角形,由此不難求出它的面積.
,△ABC是直角三角形,由此不難求出它的面積.
(2)根據(jù)正弦定理,結(jié)合題意得b2=ac,根據(jù)B= ,利用余弦定理,得b2=a2+c2-ac,從而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC為等邊三角形.
,利用余弦定理,得b2=a2+c2-ac,從而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC為等邊三角形.
試題解析:∵A、B、C成等差數(shù)列,可得2B=A+C.
∴結(jié)合A+B+C=π,可得B= .
.
(1)∵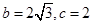 ,
,
∴由正弦定理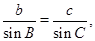 得
得 ,
,
∵b>c,可得B>C,∴C為銳角,得C=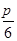 ,從而A=π-B-C=
,從而A=π-B-C=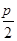 .
.
因此,△ABC的面積為S= bc=
bc= ×
×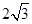 ×2=
×2=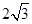 .
.
(2)∵sinA、sinB、sinC成等比數(shù)列,即sin2B=sinAsinC.
∴由正弦定理,得b2=ac
又∵根據(jù)余弦定理,得b2=a2+c2-2accosB=a2+c2-ac,
∴a2+c2-ac=ac,整理得(a-c)2=0,可得a=c
∵B= ,∴A=C=
,∴A=C= ,可得△ABC為等邊三角形.
,可得△ABC為等邊三角形.
考點:三角形內(nèi)角和定理;利用正、余弦定理;三角形的形狀判斷,等差等比數(shù)列的性質(zhì).


科目:高中數(shù)學 來源: 題型:解答題
已知公差不為0的等差數(shù)列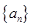 滿足
滿足 ,
,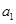 ,
,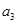 ,
,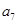 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列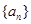 的通項公式;(2)數(shù)列
的通項公式;(2)數(shù)列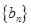 滿足
滿足 ,求數(shù)列
,求數(shù)列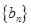 的前
的前 項和
項和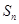 ;(Ⅲ)設(shè)
;(Ⅲ)設(shè) ,若數(shù)列
,若數(shù)列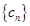 是單調(diào)遞減數(shù)列,求實數(shù)
是單調(diào)遞減數(shù)列,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
在等差數(shù)列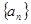 中,
中,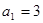 ,其前
,其前 項和為
項和為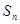 ,等比數(shù)列
,等比數(shù)列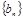 的各項均為正數(shù),
的各項均為正數(shù), ,公比為
,公比為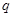 ,且
,且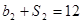 ,
,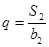 .
.
(1)求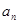 與
與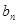 ; (2)設(shè)數(shù)列
; (2)設(shè)數(shù)列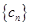 滿足
滿足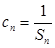 ,求
,求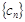 的前
的前 項和
項和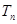 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知數(shù)列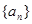 的前n項和為
的前n項和為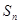 ,且
,且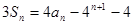
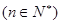 ,令
,令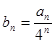 .
.
(1)求證:數(shù)列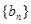 是等差數(shù)列,并求數(shù)列
是等差數(shù)列,并求數(shù)列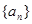 的通項公式;
的通項公式;
(2)若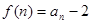
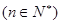 ,用數(shù)學歸納法證明
,用數(shù)學歸納法證明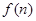 是18的倍數(shù).
是18的倍數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
數(shù)列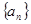 滿足:
滿足: ,
,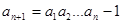 (
(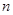 ≥3),記
≥3),記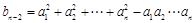
(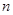 ≥3).
≥3).
(1)求證數(shù)列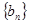 為等差數(shù)列,并求通項公式;
為等差數(shù)列,并求通項公式;
(2)設(shè) ,數(shù)列{
,數(shù)列{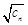 }的前n項和為
}的前n項和為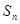 ,求證:
,求證: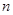 <
<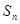 <
<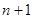 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知實數(shù)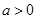 ,且
,且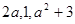 按某種順序排列成等差數(shù)列.
按某種順序排列成等差數(shù)列.
(1)求實數(shù) 的值;
的值;
(2)若等差數(shù)列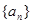 的首項和公差都為
的首項和公差都為 ,等比數(shù)列
,等比數(shù)列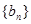 的首項和公比都為
的首項和公比都為 ,數(shù)列
,數(shù)列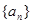 和
和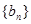 的前
的前 項和分別為
項和分別為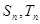 ,且
,且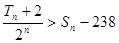 ,求滿足條件的自然數(shù)
,求滿足條件的自然數(shù) 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
打一口深20米的井,打到第一米深處時需要40分鐘,從第一米深處打到第二米深處需要50分鐘,以后每深一米都要比前一米多10分鐘,則打到最后一米深處要用 小時,打完這口井總共用 小時.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com