
【題目】某地區現有一個直角梯形水產養殖區ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在點P處有一燈塔(如圖),且點P到BC,CD的距離都是1200m,現擬將養殖區ACD分成兩塊,經過燈塔P增加一道分隔網EF,在△AEF內試驗養殖一種新的水產品,當△AEF的面積最小時,對原有水產品養殖的影響最小.設AE=d.
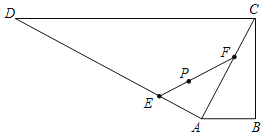
(1)若P是EF的中點,求d的值;
(2)求對原有水產品養殖的影響最小時的d的值,并求△AEF面積的最小值.
【答案】(1)480![]() ; (2)對原有水產品養殖的影響最小時,d=480
; (2)對原有水產品養殖的影響最小時,d=480![]() .△AEF面積的最小值為192000m2
.△AEF面積的最小值為192000m2
【解析】
(1)建立平面坐標系,求出直線AD,AC的方程,根據P為EF的中點列方程得出E點坐標,從而可計算d;
(2)根據基本不等式得出AEAF的最小值,進而求出△AEF的面積最小值.
解:(1)以A為坐標原點,AB所在直線為x軸,建立如圖所示的平面直角坐標系,
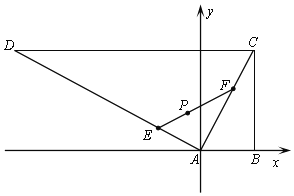
則C(800,1600),B(800,0),P(-400,400),D(-3200,1600).
AC所在直線方程為y=2x,AD所在直線方程為y=-![]() x.
x.
設E(-2m,m),F(n,2n),m>0,>0.
∵P是EF的中點,∴![]() ,解得
,解得![]() ,
,
∴E(-960,480),
∴d=|AE|=![]() =480
=480![]() .
.
(2)∵EF經過點P,∴kPE=kPF,
即![]() =
=![]() ,化簡得80m+240n=mn.
,化簡得80m+240n=mn.
由基本不等式得:mn=80m+240n≥160![]() ,
,
即mn≥76800,當且僅當m=3n=480時等號成立.
∵kACkAD=-1,∴AC⊥AD,
∴S△AEF=![]() AEAF=
AEAF=![]() m
m![]() n=
n=![]() mn≥
mn≥![]() 76800=192000,
76800=192000,
此時E(-960,480),d=AE=480![]() .
.
故對原有水產品養殖的影響最小時,d=480![]() .△AEF面積的最小值為192000m2.
.△AEF面積的最小值為192000m2.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ;
;
(1)當![]() 時,若
時,若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若定義在![]() 上的奇函數
上的奇函數![]() 滿足
滿足![]() ,且當
,且當![]() ,
,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)對于(2)中的![]() ,若關于
,若關于![]() 的不等式
的不等式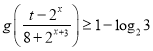 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知
中,已知![]() 平面
平面![]() ,且四邊形
,且四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() .
.

(1)證明:![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值;
所成銳二面角的余弦值;
(3)點![]() 是線段
是線段![]() 上的動點,當直線
上的動點,當直線![]() 與
與![]() 所成的角最小時,求線段
所成的角最小時,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+c(a>0),且f(1)![]() .
.
(1)求證:函數f(x)有兩個不同的零點;
(2)設x1,x2是函數f(x)的兩個不同的零點,求|x1﹣x2|的取值范圍;
(3)求證:函數f(x)在區間(0,2)內至少有一個零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 有兩個不等的實數根,求
有兩個不等的實數根,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值與最小值的差不超過1,求
上的最大值與最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,已知![]() ,且2an+1=an+1(n∈N*).
,且2an+1=an+1(n∈N*).
(1)求證:數列{an-1}是等比數列;
(2)若bn=nan,求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,直線
,直線![]() 分別交
分別交![]() 軸、
軸、![]() 軸的正半軸于
軸的正半軸于![]() 、
、![]() 兩點,
兩點,![]() 為坐標原點.
為坐標原點.
(1)若直線![]() 方程為
方程為![]() (
(![]() ),且
),且![]() ,求
,求![]() 的值;
的值;
(2)若直線![]() 經過點
經過點![]() ,設
,設![]() 的斜率為
的斜率為![]() ,
,![]() 為線段
為線段![]() 的中點,求
的中點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
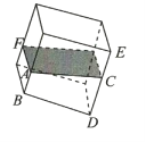
【題目】在一個長方體的容器中,里面裝有少量的水,現在將容器繞著其底部的一條棱傾斜.
(1)在傾斜的過程中,水面的形狀不斷變化,可能是矩形,也可能變成不是矩形的平行四邊形,對嗎?
(2)在傾斜的過程中,水的形狀也不斷變化,可以是棱柱,也可能變為棱臺或棱錐,對嗎?
(3)如果傾斜時,不是繞著底部的一條棱,而是繞著其底面的一個頂點,上面的第(1)問和第(2)問對不對?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com