【題目】在銳角△ABC中，
分別為A、B、C所對的邊，且
（1）確定角C的大小；
（2）若c＝
，求△ABC周長的取值范圍．
【答案】（1）C=60°；（2）（
+3
，
]．
【解析】
（1）利用正弦定理化簡已知條件，求得
的值，根據三角形是銳角三角形求得
的大小.（2）利用正弦定理將
轉化為角度來表示，求得三角形
周長的表達式，利用三角函數求取值范圍的方法，求得三角形周長的取值范圍.
解:（1）已知a、b、c分別為A、B、C所對的邊，
由
a＝2csinA，
得sinA＝2sinCsinA，又sinA≠0，則sinC=
，
∴C=60°或C=120°,
∵△ABC為銳角三角形，∴C=120°舍去。∴C=60°
（2）∵c=，sinC=
∴由正弦定理得：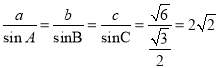
,
即a=2sinA，b=2sinB，又A+B=π-C=
，
即B=-A
∴a+b+c=2（sinA+sinB）+=2 [sinA+sin（-A）]+
=2（sinA+sincosA-cossinA）+
=2（sinAcos
+cosAsin）+=2sin（A+）+，
∵△ABC是銳角三角形，
∴＜A＜
，
∴＜sin（A+）≤1，
則△ABC周長的取值范圍是（+3，]．
課時訓練江蘇人民出版社系列答案
黃岡經典趣味課堂系列答案科目：高中數學 來源： 題型：
【題目】為了了解學生的學習情況，一次測試中，科任老師從本班中抽取了n個學生的成績（滿分100分，且抽取的學生成績均在
內）進行統計分析.按照
，
，
，
，
，
的分組作出頻率分布直方圖和頻數分布表.
頻數分布表 | |
| x |
| 4 |
| 10 |
| 12 |
| 8 |
| 4 |
（1）求n，a，x的值；
（2）在選取的樣本中，從低于60分的學生中隨機抽取兩名學生，試問這兩名學生在同一組的概率是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，以
軸為始邊做兩個銳角
，它們的終邊分別與單位圓相交于A，B兩點，已知A，B的橫坐標分別為
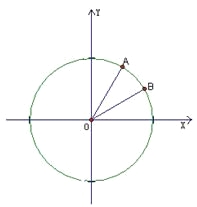
（1）求
的值； （2）求
的值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區2008年至2016年糧食產量的部分數據如下表：
（1）求該地區2008年至2016年的糧食年產量
與年份
之間的線性回歸方程；
（2）利用（1）中的回歸方程，分析2008年至2016年該地區糧食產量的變化情況，并預測該地區 2018年的糧食產量.
附:回歸直線的斜率和截距的最小二乘估計公式分別為
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
有如下性質：如果常數
，那么該函數在
上是減函數，在
是增函數，其圖像如圖所示．
(1)已知
，
，利用上述性質，求函數
的單調區間和值域；
(2)對于(1)中的函數和函數
，若對任意
，總存在
，使得
成立，求實數
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
