
【題目】在一個長方體的容器中,里面裝有少量的水,現在將容器繞著其底部的一條棱傾斜.
(1)在傾斜的過程中,水面的形狀不斷變化,可能是矩形,也可能變成不是矩形的平行四邊形,對嗎?
(2)在傾斜的過程中,水的形狀也不斷變化,可以是棱柱,也可能變為棱臺或棱錐,對嗎?
(3)如果傾斜時,不是繞著底部的一條棱,而是繞著其底面的一個頂點,上面的第(1)問和第(2)問對不對?
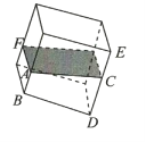
【答案】(1)可以是矩形,但不可能是其他非矩形的平行四邊形(2)水比較少時,是三棱柱,水多時,可能是四棱柱,或五棱柱;但不可能是棱臺或棱錐.(3)(1)對,(2)不對.
【解析】
根據繞著棱旋轉和繞著點旋轉的特點,將問題轉化為長方體被相應平面所截形成的截面形狀.
(1)不對.水面的形狀就是用一個與棱(長方體容器傾斜時固定不動的棱)平行的平面截長方體時截面的形狀,因而可以是矩形,但不可能是其他非矩形的平行四邊形.
(2)不對.水的形狀就是用與棱(長方體容器傾斜時固定不動的棱)平行的平面將長方體截去一部分后,剩余部分的幾何體,此幾何體是棱柱,水比較少時,是三棱柱,水多時,可能是四棱柱,或五棱柱;但不可能是棱臺或棱錐.
(3)用任意一個平面去截長方體,其截面形狀可以是三角形,四邊形,五邊形,六邊形,因而水面的形狀可以是三角形,四邊形,五邊形,六邊形;水的形狀可以是棱錐,棱柱,但不可能是棱臺.故(1)對,(2)不對.


科目:高中數學 來源: 題型:
【題目】某地區現有一個直角梯形水產養殖區ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在點P處有一燈塔(如圖),且點P到BC,CD的距離都是1200m,現擬將養殖區ACD分成兩塊,經過燈塔P增加一道分隔網EF,在△AEF內試驗養殖一種新的水產品,當△AEF的面積最小時,對原有水產品養殖的影響最小.設AE=d.
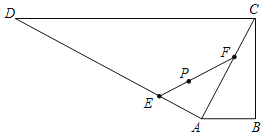
(1)若P是EF的中點,求d的值;
(2)求對原有水產品養殖的影響最小時的d的值,并求△AEF面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,對于定義域內的任意實數
,對于定義域內的任意實數![]() ,有
,有![]() 成立,且
成立,且![]() 時,
時,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的最大值;
的最大值;
(2)當![]() 時,求函數
時,求函數![]() 的最大值;
的最大值;
(3)已知![]() (實數
(實數![]() ),求實數
),求實數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖表示一位騎自行車者和一位騎摩托車者在相距![]() 的兩城鎮間旅行的函數圖象,由圖,可知騎自行車者用了
的兩城鎮間旅行的函數圖象,由圖,可知騎自行車者用了![]() ,沿途休息了
,沿途休息了![]() ,騎摩托車者用了
,騎摩托車者用了![]() ,根據這個圖象,提出關于這兩個旅行者的如下信息:
,根據這個圖象,提出關于這兩個旅行者的如下信息:

①騎自行車者比騎摩托車者早出發![]() ,晚到
,晚到![]() ;
;
②騎自行車者是變速運動,騎摩托者是勻速運動;
③騎摩托車者在出發了![]() 后,追上了騎自行車者.
后,追上了騎自行車者.
其中正確信息的序號是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() .
.![]() 是自然對數的底數.
是自然對數的底數.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .求實數
.求實數![]() 的值;
的值;
(2)① 若![]() 時,函數
時,函數![]() 既有極大值,又有極小值,求實數
既有極大值,又有極小值,求實數![]() 的取值范圍;
的取值范圍;
② 若![]() ,
,![]() .若
.若![]() 對一切正實數
對一切正實數![]() 恒成立,求實數
恒成立,求實數![]() 的最大值(用
的最大值(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知無窮數列{an}(an∈Z)的前n項和為Sn,記S1,S2,…,Sn中奇數的個數為bn.
(1)若an=n,請寫出數列{bn}的前5項;
(2)求證:“a1為奇數,ai(i=2,3,4,…)為偶數”是“數列{bn}是單調遞增數列”的充分不必要條件;
(3)若ai=bi,i=1,2,3,…,求數列{an}的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com