Question

【題目】十九大以來，某貧困地區扶貧辦積極貫徹落實國家精準扶貧的政策要求，帶領廣大農村地區人民群眾脫貧奔小康。經過不懈的奮力拼搏，新農村建設取得巨大進步，農民年收入也逐年增加。為了更好的制定2019年關于加快提升農民年收人力爭早日脫貧的工作計劃，該地扶貧辦統計了2018年位農民的年收人并制成如下頻率分布直方圖：

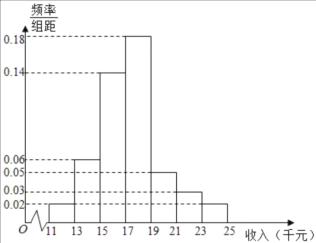
（1）根據頻率分布直方圖，估計位農民的年平均收入（單位：千元）（同一組數據用該組數據區間的中點值表示）；

（2）由頻率分布直方圖，可以認為該貧困地區農民年收入服從正態分布，其中近似為年平均收入，近似為樣本方差，經計算得.利用該正態分布，求:

(i)在2019年脫貧攻堅工作中，若使該地區約有占總農民人數的的農民的年收入高于扶貧辦制定的最低年收入標準，則最低年收入大約為多少千元？

（ii）為了調研“精準扶貧，不落一人”的政策要求落實情況，扶貧辦隨機走訪了位農民。若每個農民的年收人相互獨立，問：這位農民中的年收入不少于千元的人數最有可能是多少？

附：參考數據與公式

則①；②；③.

Answer 1

【答案】(1)17.40千元 (2)(i)千元（ii）978

【解析】

（1）取出每一組數據中間值，充當，利用公式進行求解即可

（2）根據正態分布特征值，結合附表所給內容，可判斷，再計算出對應的值即可

（3）由題中位農民中的年收入不少于千元，即，記個農民的年收入不少于千元的人數為，則，再根據二項分布的概率公式，結合“精準扶貧，不落一人”的特點來進行判斷即可

解：千元.

由題意，.

（i）時，滿足題意即最低年收入大約為千元

（ii）由，得

每個農民的年收入不少于千元的事件概率為，

記個農民的年收入不少于千元的人數為，則，其中，

于是恰好有個農民的年收入不少于千元的事件概率是

從而由，得

而，所以，當時，

當時，

由此可知，在所走訪的位農民中，年收入不少于千元的人數最有可能是