【題目】已知數(shù)列1、1、2、1、2、4、1、2、4、8、1、2、4、8、16、…，其中第一項(xiàng)是
，接下來(lái)的兩項(xiàng)是、
，再接下來(lái)的三項(xiàng)是、、
，以此類(lèi)推，若
且該數(shù)列的前
項(xiàng)和為2的整數(shù)冪，則的最小值為（ ）
A.440B.330C.220D.110
【答案】A
【解析】
把題設(shè)中的數(shù)列分成如下的組：
，記前
組的和為
，算出后結(jié)合前
項(xiàng)和為2的整數(shù)冪可得的最小值.
把題設(shè)中的數(shù)列分成如下的組： ，記前組的和為。
則
.
令
即
，故
.
故當(dāng)
時(shí)，數(shù)列至少包括前13組且含有第14組的前
個(gè)元素.
設(shè)前項(xiàng)和為2的整數(shù)冪且第項(xiàng)為第組的第
個(gè)元素，則
，
且前項(xiàng)和
，其中
，.
下證：當(dāng)時(shí)，總有
.
記
，則當(dāng)時(shí)，有
，
故
為單調(diào)增數(shù)列，而
，故
即.
所以
，
由
為2的整數(shù)冪，故
，從而
，
當(dāng)
時(shí)，
，與
矛盾；
當(dāng)
時(shí)，
，此時(shí)
，
故選：A.
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知各項(xiàng)均為正數(shù)的數(shù)列
的前
項(xiàng)和為
且滿足:
(1)求數(shù)列的通項(xiàng)公式；
(2)設(shè)
求
的值；
(3)是否存在大于2的正整數(shù)
使得
?若存在,求出所有符合條件的
若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】下面有五個(gè)命題：
①函數(shù)
的最小正周期是
；
②終邊在
軸上的角的集合是
；
③在同一坐標(biāo)系中，函數(shù)
的圖象和函數(shù)
的圖象有三個(gè)公共點(diǎn)；
④把函數(shù)
的圖象向右平移
個(gè)單位得到
的圖象；
⑤函數(shù)
在
上是減函數(shù)；
其中真命題的序號(hào)是（ ）
A.①②⑤B.①④C.③⑤D.②④
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】關(guān)于函數(shù)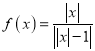
，給出以下四個(gè)命題：（1）當(dāng)
時(shí)，
單調(diào)遞減且沒(méi)有最值；（2）方程
一定有實(shí)數(shù)解；（3）如果方程
（
為常數(shù)）有解，則解得個(gè)數(shù)一定是偶數(shù)；（4）是偶函數(shù)且有最小值.其中假命題的序號(hào)是____________.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，矩形
是一個(gè)歷史文物展覽廳的俯視圖，點(diǎn)
在
上，在梯形
區(qū)域內(nèi)部展示文物，
是玻璃幕墻，游客只能在
區(qū)域內(nèi)參觀．在
上點(diǎn)
處安裝一可旋轉(zhuǎn)的監(jiān)控?cái)z像頭．
為監(jiān)控角，其中
、
在線段（含端點(diǎn)）上，且點(diǎn)在點(diǎn)的右下方．經(jīng)測(cè)量得知：
米，
米，
米，
．記
(弧度)，監(jiān)控?cái)z像頭的可視區(qū)域
的面積為
平方米．
（1）求關(guān)于
的函數(shù)關(guān)系式，并寫(xiě)出的取值范圍；（參考數(shù)據(jù)：
）
（2）求的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知全集為
，
，定義集合
的特征函數(shù)為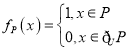
，對(duì)于
，
，給出下列四個(gè)結(jié)論:
（1）對(duì)任意
，有
（2）對(duì)任意，若
，則
（3）對(duì)任意，有
（4）對(duì)任意，有
其中，正確的序號(hào)是_____
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】某游戲棋盤(pán)上標(biāo)有第
、
、
、
、
站，棋子開(kāi)始位于第站，選手拋擲均勻硬幣進(jìn)行游戲，若擲出正面，棋子向前跳出一站；若擲出反面，棋子向前跳出兩站，直到跳到第
站或第站時(shí)，游戲結(jié)束.設(shè)游戲過(guò)程中棋子出現(xiàn)在第
站的概率為
.
（1）當(dāng)游戲開(kāi)始時(shí)，若拋擲均勻硬幣
次后，求棋子所走站數(shù)之和
的分布列與數(shù)學(xué)期望；
（2）證明：
；
（3）若最終棋子落在第站，則記選手落敗，若最終棋子落在第站，則記選手獲勝.請(qǐng)分析這個(gè)游戲是否公平.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】關(guān)于函數(shù)的對(duì)稱(chēng)性有如下結(jié)論：對(duì)于給定的函數(shù)
，如果對(duì)于任意的
都有
成立
為常數(shù)），則函數(shù)
關(guān)于點(diǎn)
對(duì)稱(chēng)．
（1）用題設(shè)中的結(jié)論證明：函數(shù)
關(guān)于點(diǎn)
；
（2）若函數(shù)既關(guān)于點(diǎn)
對(duì)稱(chēng)，又關(guān)于點(diǎn)
對(duì)稱(chēng)，且當(dāng)
時(shí)，
，求：①
的值；
②當(dāng)
時(shí)，的表達(dá)式．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】在三棱錐
中，OA、OB、OC所在直線兩兩垂直，且
，CA與平面AOB所成角為
，D是AB中點(diǎn)，三棱錐的體積是
．
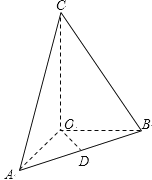
（1）求三棱錐的高；
（2）在線段CA上取一點(diǎn)E，當(dāng)E在什么位置時(shí)，異面直線BE與OD所成的角為
？
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com