
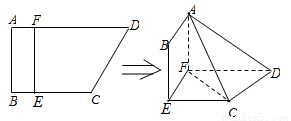
(本題滿分12分)如圖,四邊形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分別在BC、AD上,EF∥AB.現將四邊形ABEF沿EF折起,使得平面ABEF  平面EFDC.
平面EFDC.
(1)當 ,是否在折疊后的AD上存在一點
,是否在折疊后的AD上存在一點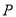 ,使得CP∥平面ABEF?若存在,求出P點位置,若不存在,說明理由;
,使得CP∥平面ABEF?若存在,求出P點位置,若不存在,說明理由;
(2)設BE=x,問當x為何值時,三棱錐A CDF的體積有最大值?并求出這個最大值.
CDF的體積有最大值?并求出這個最大值.
(1)存在,且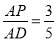 ;(2)當x=3時,
;(2)當x=3時,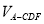 有最大值,最大值為3.
有最大值,最大值為3.
【解析】
試題分析:(1)當 時,由題意可知
時,由題意可知 ,則考慮取點
,則考慮取點 于
于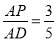 處,過點
處,過點 作
作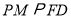 ,交
,交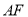 于點
于點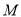 ,由平行線分段成比例定理易知
,由平行線分段成比例定理易知 ,所以
,所以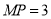 ,又因為
,又因為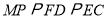 ,所以
,所以 且
且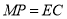 ,
,
(2)根據題意易知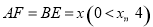 為三棱錐
為三棱錐 的高,則底面
的高,則底面 的長為
的長為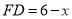 ,高為
,高為 ,所以
,所以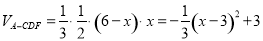 ,從而可求出當
,從而可求出當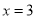 時,
時,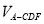 有最大值,最大值為3.
有最大值,最大值為3.
試題解析:(1)存在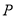 使得滿足條件CP∥平面ABEF,且此時.
使得滿足條件CP∥平面ABEF,且此時.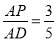 2分
2分
下面證明: 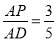 ,過點
,過點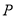 作MP∥FD,與AF交于點
作MP∥FD,與AF交于點 ,則有
,則有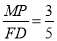 ,又FD=
,又FD=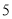 ,故MP=3,又因為EC=3,MP∥FD∥EC,故有MP
,故MP=3,又因為EC=3,MP∥FD∥EC,故有MP EC,故四邊形MPCE為平行四邊形,所以PC∥ME,又CP
EC,故四邊形MPCE為平行四邊形,所以PC∥ME,又CP 平面ABEF,ME
平面ABEF,ME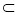 平面ABEF,故有CP∥平面ABEF成立. 6分
平面ABEF,故有CP∥平面ABEF成立. 6分
(2)因為平面ABEF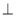 平面EFDC,平面ABEF
平面EFDC,平面ABEF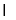 平面EFDC=EF,又AF
平面EFDC=EF,又AF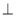 EF,所以AF⊥平面EFDC.
EF,所以AF⊥平面EFDC.
由已知BE=x,,所以AF=x(0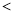 x
x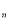 4),FD=6
4),FD=6 x.
x.
故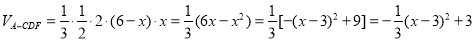 .所以,當x=3時,
.所以,當x=3時,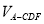 有最大值,最大值為3.
有最大值,最大值為3.
考點:1.平面圖形與立體圖形的轉化;2.線面平行的判定;3.三棱錐的體積.


科目:高中數學 來源: 題型:
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、?x≤0,都有x2-x>0 | B、?x>0,都有x2-x≤0 | C、?x>0,使得x2-x<0 | D、?x≤0,使得x2-x>0 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、60種 | B、42種 | C、36種 | D、24種 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、24 | B、36 | C、40 | D、44 |
查看答案和解析>>
科目:高中數學 來源:2015屆遼寧省五校協作體高三上學期期中考試理科數學試卷(解析版) 題型:選擇題
已知函數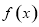 在
在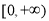 上可導,其導函數記作
上可導,其導函數記作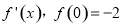 ,且
,且 ,當
,當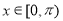 時,
時, ,若方程
,若方程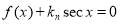 在[0,+∞)上有n個解,則數列
在[0,+∞)上有n個解,則數列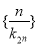 的前n項和為( )
的前n項和為( )
A.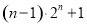 B.
B.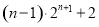 C.
C.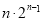 D.
D.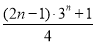
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com