
設函數 
(Ⅰ)若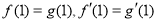 ,是否存在k和m,使得
,是否存在k和m,使得 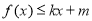 ,
, ,若存在,求出k和m的值,若不存在,說明理由
,若存在,求出k和m的值,若不存在,說明理由
(Ⅱ)設  有兩個零點
有兩個零點  ,且
,且  成等差數列,
成等差數列, 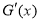 是 G (x)的導函數,求證:
是 G (x)的導函數,求證: 
(Ⅰ) 存在k=2,m=-1;(Ⅱ)見解析
【解析】
試題分析:(Ⅰ) 先求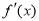 ,然后根據條件很容易求出a,b,此時會發現
,然后根據條件很容易求出a,b,此時會發現 和
和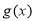 圖象有一個公共點(1,1),根據問題:是否存在k和m,使得
圖象有一個公共點(1,1),根據問題:是否存在k和m,使得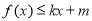 ,
, ,也就是找到一條直線要同時滿足這兩個不等式.根據存在的公共點可以想到是否是過這一點的直線,故先求出還
,也就是找到一條直線要同時滿足這兩個不等式.根據存在的公共點可以想到是否是過這一點的直線,故先求出還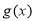 在(1,1)的切線,然后去驗證它是否同時滿足
在(1,1)的切線,然后去驗證它是否同時滿足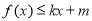 ,
, 即可.(Ⅱ)先求出
即可.(Ⅱ)先求出 ,根據條件x1,x2是它的兩個零點,所以x12?alnx1?bx1+2=0且x22?alnx2?bx2+2=0.根據所要證的結論:
,根據條件x1,x2是它的兩個零點,所以x12?alnx1?bx1+2=0且x22?alnx2?bx2+2=0.根據所要證的結論: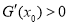 ,所以需要求
,所以需要求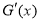 ,利用x1+x2=2x0,將
,利用x1+x2=2x0,將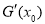 用x1,x2表示出來,然后判斷它是否大于0即可.
用x1,x2表示出來,然后判斷它是否大于0即可.
試題解析:(Ⅰ)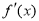 =
=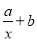 ,
,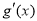 =
=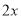 ,由
,由 得:a+b=2, b=1,解得,解得a=b=1.∴
得:a+b=2, b=1,解得,解得a=b=1.∴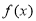 =
=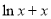 .
.
因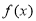 與
與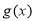 有一個公共點(1,1),易求得函數
有一個公共點(1,1),易求得函數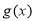 =
=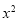 在點(1,1)的切線方程為
在點(1,1)的切線方程為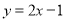 .
.
下面驗證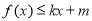 ,
, 都成立即可.
都成立即可.
設h(x)=lnx+x-(2x-1)=lnx-x+1,所以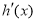 =
=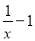 =
=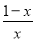 .
.
x∈(0,1)時,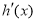 >0;x∈(1,+∞)時,
>0;x∈(1,+∞)時,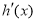 <0,∴x=1時,
<0,∴x=1時, 取最大值
取最大值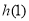 =0;
=0;
∴lnx+x≤2x-1恒成立,即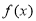 ≤
≤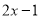 2.
2.
由于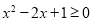 ,得
,得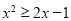 ,∴
,∴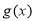 ≥
≥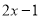 恒成立.
恒成立.
故存在這樣的k,m,且k=2,m=-1. 6分
(Ⅱ) 因為 =
=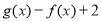 =
=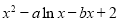 ,有兩個零點x1,x2,
,有兩個零點x1,x2,
則x12?alnx1?bx1+2=0且x22?alnx2?bx2+2=0,
兩式相減得,x12? x22-a(lnx1? lnx2)-b(x1?x2)=0,
所以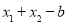 =
=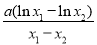 ,又因為x1+x2=2x0,
,又因為x1+x2=2x0,
因為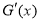 =
=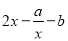 ,所以
,所以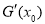 =
=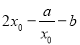 =
=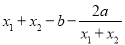 =
=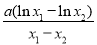
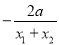
=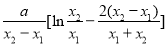 =
= ,
,
當0<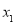 <
<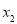 時,令
時,令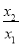 =
=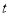 ,則
,則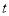 >1,且
>1,且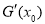 =
=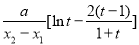 ,
,
設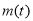 =
=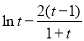 (t>1),所以
(t>1),所以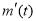 =
=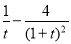 =
=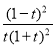 >0,所以
>0,所以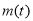 在[1,+
在[1,+ )上是增函數,
)上是增函數,
所以當t>1時,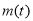 >
>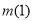 =0,即
=0,即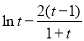 >0,
>0,
又因為a>0,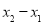 >0,所以
>0,所以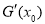 >0,
>0,
當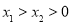 時,同理可證
時,同理可證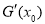 >0,
>0,
綜上所述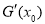 >0, 12分
>0, 12分
考點:常見函數的導數,導數的運算法則,函數的切線,函數零點,導數的綜合運用,運算求解能力,推理論證能力,轉化與化歸思想


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源:2013-2014學年河南省長葛市畢業班第三次質量預測(三模)文科數學試卷(解析版) 題型:解答題
如圖,三棱柱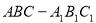 的側棱
的側棱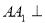 平面
平面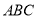 ,
,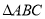 為等邊三角形,側面
為等邊三角形,側面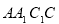 是正方形,
是正方形,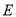 是
是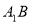 的中點,
的中點,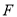 是棱
是棱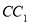 上的點.
上的點.
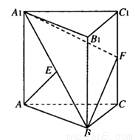
(1)若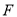 是棱
是棱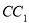 中點時,求證:
中點時,求證: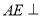 平面
平面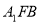 ;
;
(2)當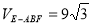 時,求正方形
時,求正方形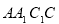 的邊長.
的邊長.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河南省鄭州市高三第二次模擬考試文科數學試卷(解析版) 題型:選擇題
已知雙曲線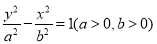 的兩個焦點分別為
的兩個焦點分別為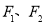 ,以線段
,以線段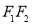 直徑的圓與雙曲線漸近線的一個交點為
直徑的圓與雙曲線漸近線的一個交點為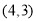 .則此雙曲線的方程為
.則此雙曲線的方程為
A.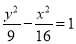 B.
B.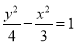 C.
C.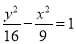 D.
D.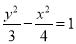
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河南省畢業班高考適應性模擬練習理科數學試卷(解析版) 題型:選擇題
已知命題p:?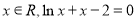 ,命題q:?
,命題q:?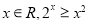 ,則下列命題中為真命題的是()
,則下列命題中為真命題的是()
A.p∧q B.?p∧q C.p∧?q D.?p∧?q
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河南省原名校高三高考仿真模擬統一考試理科數學試卷(解析版) 題型:填空題
已知數列 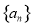 的前n項和為
的前n項和為 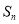 ,滿足
,滿足 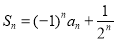 ,
, 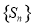 的前n項和為
的前n項和為 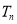 ,則
,則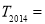 _________.
_________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河南省原名校高三高考仿真模擬統一考試理科數學試卷(解析版) 題型:選擇題
設 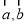 為單位向量,若
為單位向量,若 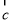 滿足
滿足 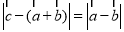 ,則
,則  的最大值為
的最大值為
A. B.2 C.
B.2 C.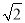 D.1
D.1
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河南省原名校高三高考仿真模擬統一考試文科數學試卷(解析版) 題型:填空題
我們把焦點相同,且離心率互為倒數的橢圓和雙曲線稱為一對“相關曲線”,己知 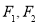 是一對相關曲線的焦點,P是它們在第一象限的交點,當
是一對相關曲線的焦點,P是它們在第一象限的交點,當 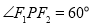 ,則這 一對相關曲線中橢圓的離心率是________.
,則這 一對相關曲線中橢圓的離心率是________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省邯鄲市高三第二次模擬考試理科數學試卷(解析版) 題型:解答題
已知圓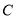 的極坐標方程為
的極坐標方程為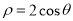 ,直線
,直線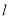 的參數方程為
的參數方程為
(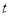 為參數),點
為參數),點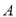 的極坐標為
的極坐標為 ,設直線
,設直線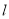 與圓
與圓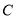 交于點
交于點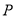 、
、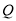 .
.
(1)寫出圓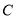 的直角坐標方程;
的直角坐標方程;
(2)求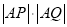 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com