Question

10．正方體ABCD-A₁B₁C₁D₁的棱長為6，點O在BC上，且BO=OC，過點O的直線l與直線AA₁，C₁D₁分別交于M，N兩點，則MN與面ADD₁A₁所成角的正弦值為（　　）

• A． $\frac{2}{3}$
• B． $\frac{\sqrt{3}}{2}$
• C． $\frac{\sqrt{2}}{2}$
• D． $\frac{\sqrt{3}}{3}$

Answer 1

分析 設(shè)MD₁交AD于E，根據(jù)C₁D₁∥平面ABCD可得C₁D₁∥OE，從而E為AD的中點，故可計算出MD₁和ND₁，從而可求出sin∠NMD₁．

解答 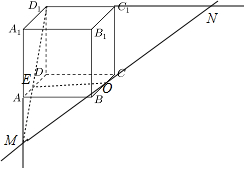解：∵C₁D₁⊥平面ADD₁A₁，
∴∠NMD₁是MN與面ADD₁A₁所成角，
設(shè)MD₁與AD交點為E，連結(jié)OE，
∵C₁D₁∥平面ABCD，C₁D₁?平面MND₁，平面MND₁∩平面ABCD=DE，
∴C₁D₁∥OE，
∵O是BC的中點，∴E是AD的中點，
∴E是MD₁的中點，MD₁=2ED₁=6$\sqrt{5}$，
∴ND₁=2OE=12，∴MN=$\sqrt{1{2}^{2}+（6\sqrt{5}）^{2}}$=18，
∴sin∠NMD₁=$\frac{N{D}_{1}}{MN}$=$\frac{2}{3}$．
故選A．

點評 本題考查了線面平行的性質(zhì)，線面角的計算，屬于中檔題．