
【題目】已知函數![]() 圖像上一點
圖像上一點![]() 處的切線方程為
處的切線方程為![]()
(1)求![]() 的值;
的值;
(2)若方程![]() 在區間
在區間![]() 內有兩個不等實根,求
內有兩個不等實根,求![]() 的取值范圍;
的取值范圍;
(3)令![]() 如果
如果![]() 的圖像與
的圖像與![]() 軸交于
軸交于![]() 兩點,
兩點,![]() 的中點為
的中點為![]() ,求證:
,求證:![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析
;(3)證明見解析
【解析】
(1)根據導數的幾何意義可知![]() ,利用切線方程求得
,利用切線方程求得![]() ,代入曲線可得關于
,代入曲線可得關于![]() 的方程,與
的方程,與![]() 聯立可構造方程組求得結果;(2)將問題轉化為
聯立可構造方程組求得結果;(2)將問題轉化為![]() 與
與![]() 的圖象在
的圖象在![]() 上有兩個交點;利用導數得到
上有兩個交點;利用導數得到![]() 在
在![]() 上的單調性和最值,從而確定有兩個交點時
上的單調性和最值,從而確定有兩個交點時![]() 的取值范圍,進而得到結果;(3)采用反證法,假設
的取值范圍,進而得到結果;(3)采用反證法,假設![]() ,利用
,利用![]() 在
在![]() 上,中點坐標公式和
上,中點坐標公式和![]() 可化簡整理得到
可化簡整理得到 ,令
,令![]() ,構造函數
,構造函數![]() ,利用導數可知
,利用導數可知![]() 在
在![]() 上單調遞增,從而得到
上單調遞增,從而得到![]() ,與等式矛盾,可知假設不成立,從而證得結論.
,與等式矛盾,可知假設不成立,從而證得結論.
由題意得:![]() 定義域為
定義域為![]() ;
;![]()
(1)![]() 在
在![]() 處的切線方程為:
處的切線方程為:![]()
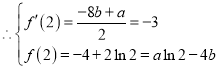 ,解得:
,解得:![]()
(2)方程![]() 在區間
在區間![]() 內有兩個不等實根等價于
內有兩個不等實根等價于![]() 與
與![]() 的圖象在
的圖象在![]() 上有兩個交點
上有兩個交點
由(1)知:![]() ,
,![]()
![]() 當
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減
上單調遞減 ![]()
又![]() ,
,![]()
![]() ,解得:
,解得:![]()
(3)![]() ,則
,則![]()
假設![]() ,則有:
,則有:
![]() …①;
…①;![]() …②;
…②;
![]() …③;
…③;![]() …④
…④
①![]() ②得:
②得:![]()
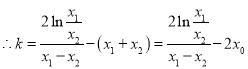
由④得:![]()
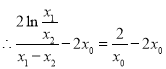 ,即:
,即: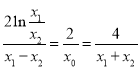
 ,即
,即
令![]() ,由
,由![]() 得:
得:![]()
設![]() ,
,![]()

![]() 在
在![]() 上單調遞增
上單調遞增 ![]()
![]()
 不成立,即假設不成立
不成立,即假設不成立
![]()


科目:高中數學 來源: 題型:
【題目】如圖所示,合肥一中積極開展美麗校園建設,現擬在邊長為0.6千米的正方形地塊![]() 上劃出一片三角形地塊
上劃出一片三角形地塊![]() 建設小型生態園,點
建設小型生態園,點![]() 分別在邊
分別在邊![]() 上.
上.
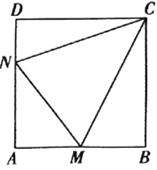
(1)當點![]() 分別時邊
分別時邊![]() 中點和
中點和![]() 靠近
靠近![]() 的三等分點時,求
的三等分點時,求![]() 的余弦值;
的余弦值;
(2)實地勘察后發現,由于地形等原因,![]() 的周長必須為1.2千米,請研究
的周長必須為1.2千米,請研究![]() 是否為定值,若是,求此定值,若不是,請說明理由.
是否為定值,若是,求此定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平面四邊形ABCD中,E、F是AD、BD中點,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,將△ABD沿對角線BD折起至△
,∠BDC=90°,將△ABD沿對角線BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,則四面體
⊥平面BCD,則四面體![]() 中,下列結論不正確是 ( )
中,下列結論不正確是 ( )
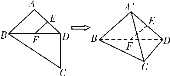
A. EF∥平面![]()
B. 異面直線CD與![]() 所成的角為90°
所成的角為90°
C. 異面直線EF與![]() 所成的角為60°
所成的角為60°
D. 直線![]() 與平面BCD所成的角為30°
與平面BCD所成的角為30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 圖像上一點
圖像上一點![]() 處的切線方程為
處的切線方程為![]()
(1)求![]() 的值;
的值;
(2)若方程![]() 在區間
在區間![]() 內有兩個不等實根,求
內有兩個不等實根,求![]() 的取值范圍;
的取值范圍;
(3)令![]() 如果
如果![]() 的圖像與
的圖像與![]() 軸交于
軸交于![]() 兩點,
兩點,![]() 的中點為
的中點為![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() 平面ABCD,四邊形ABCD是矩形,且
平面ABCD,四邊形ABCD是矩形,且![]() ,
,![]() ,E是棱BC上的動點,F是線段PE的中點.
,E是棱BC上的動點,F是線段PE的中點.
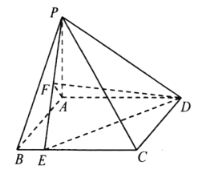
(Ⅰ)求證:![]() 平面ADF;
平面ADF;
(Ⅱ)若直線DE與平面ADF所成角為30°,求EC的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘數學家阿波羅尼奧斯(約公元前262~公元前190年)的著作《圓錐曲線論》是古代世界光輝的科學成果,他證明過這樣一個命題:平面內與兩定點距離的比為常數k(k>0,k≠1)的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.在平面直角坐標系中,設A(﹣3,0),B(3,0),動點M滿足![]() =2,則動點M的軌跡方程為()
=2,則動點M的軌跡方程為()
A. (x﹣5)2+y2=16B. x2+(y﹣5)2=9
C. (x+5)2+y2=16D. x2+(y+5)2=9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD-A1B1C1D1中,E,F分別是C1D1,CC1的中點,則異面直線AE與BF所成角的余弦值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com