

科目:高中數學 來源:不詳 題型:解答題
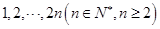 的右焦點
的右焦點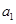 ,點
,點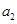 分別在
分別在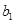 的兩條漸近線上,
的兩條漸近線上,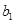 軸,
軸,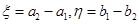 ∥
∥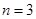 (
(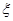 為坐標原點).
為坐標原點).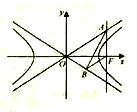
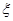 的方程;
的方程;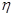 上一點
上一點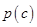 的直線
的直線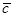 與直線
與直線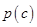 相交于點
相交于點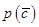 ,與直線
,與直線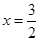 相交于點
相交于點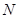 ,證明點
,證明點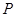 在
在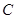 上移動時,
上移動時,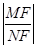 恒為定值,并求此定值.
恒為定值,并求此定值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
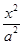 -
- =1(a>0,b>0)的一條漸近線方程是y=
=1(a>0,b>0)的一條漸近線方程是y=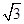 x,它的一個焦點與拋物線y2=16x的焦點相同,則雙曲線的方程為________.
x,它的一個焦點與拋物線y2=16x的焦點相同,則雙曲線的方程為________.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
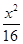 -
-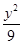 =1上,點Q在曲線C2:(x-5)2+y2=1上,點R在曲線C3:(x+5)2+y2=1上,則|PQ|-|PR|的最大值是________.
=1上,點Q在曲線C2:(x-5)2+y2=1上,點R在曲線C3:(x+5)2+y2=1上,則|PQ|-|PR|的最大值是________.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com