
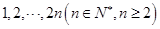 ���ҽ��c(di��n)
���ҽ��c(di��n)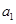 ,�c(di��n)
,�c(di��n)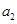 �քe��
�քe�� �ăɗl�u�����ϣ�
�ăɗl�u�����ϣ�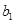 �S��
�S��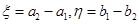 ��
��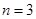 (
(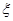 ������(bi��o)ԭ�c(di��n)��.
������(bi��o)ԭ�c(di��n)��.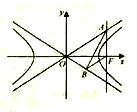
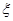 �ķ��̣�
�ķ��̣�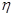 ��һ�c(di��n)
��һ�c(di��n)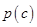 ��ֱ��
��ֱ��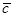 �cֱ��
�cֱ��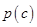 �ཻ���c(di��n)
�ཻ���c(di��n)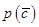 ���cֱ��
���cֱ��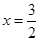 �ཻ���c(di��n)
�ཻ���c(di��n)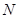 ���C���c(di��n)
���C���c(di��n)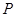 ��
��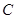 ���Ƅ�(d��ng)�r(sh��)��
���Ƅ�(d��ng)�r(sh��)��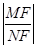 ��鶨ֵ������˶�ֵ.
��鶨ֵ������˶�ֵ. ��2��
��2��
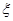 �ķ��̾���Ҫ�_��a��ֵ����a,c��ʾ�l����
�ķ��̾���Ҫ�_��a��ֵ����a,c��ʾ�l����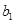 �S��
�S��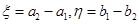 ��
��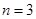 �����ɵã�ֱ��OB���̞�
�����ɵã�ֱ��OB���̞�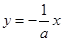 ��ֱ��BF�ķ��̞�
��ֱ��BF�ķ��̞�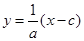 �����
�����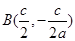 ��ֱ��OA�ķ��̞�
��ֱ��OA�ķ��̞� ���t
���t ����?y��n)�AB
����?y��n)�AB OB������
OB������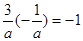 �����
�����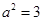 �����p����C�ķ��̞�
�����p����C�ķ��̞� ��2�����}�C����(sh��)�|(zh��)��Ӌ(j��)��
��2�����}�C����(sh��)�|(zh��)��Ӌ(j��)��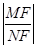 ��ֵ.�քe������(bi��o)��ʾֱ��
��ֵ.�քe������(bi��o)��ʾֱ�� �cAF�Ľ��c(di��n)
�cAF�Ľ��c(di��n)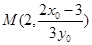 ��ֱ��
��ֱ��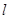 �cֱ��
�cֱ��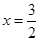 �Ľ��c(di��n)��
�Ľ��c(di��n)�� ��������
��������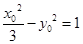 ����(ji��n).��
����(ji��n).�� .
.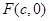 ����?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824053806114352.png" style="vertical-align:middle;" />������
����?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824053806114352.png" style="vertical-align:middle;" />������
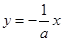 ��ֱ��BF�ķ��̞�
��ֱ��BF�ķ��̞�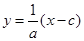 �����
�����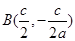
 ���t
���t
 OB������
OB������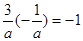 �����
�����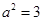 �����p����C�ķ��̞�
�����p����C�ķ��̞�
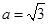 ���tֱ��
���tֱ�� �ķ��̞�
�ķ��̞�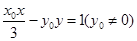 ����
����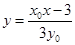
 ������ֱ��
������ֱ��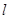 �cAF�Ľ��c(di��n)
�cAF�Ľ��c(di��n)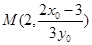
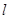 �cֱ��
�cֱ��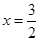 �Ľ��c(di��n)��
�Ľ��c(di��n)��
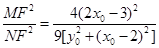
 ��������ʽ��
��������ʽ�� ������ֵ��
������ֵ��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
A�� | B��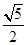 | C��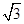 | D��2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
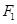 ��
��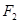 ���c(di��n)A��C�ϣ���
���c(di��n)A��C�ϣ���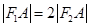 ���t
���t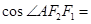 �� ��
�� ��A��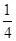 | B��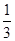 | C��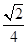 | D��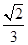 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
 ��һ�l�u�����c����(sh��)
��һ�l�u�����c����(sh��)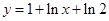 �ĈD�����У��t�p����
�ĈD�����У��t�p���� ���x���ʵ��ڣ� ��
���x���ʵ��ڣ� ��A��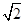 | B�� 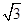 | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
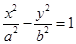 (a>0��b>0)�����ҽ��c(di��n)���^F1�Ҵ�ֱ��x�S��ֱ���c�p��������A��B���c(di��n)������ABF2���J�������Σ��tԓ�p�����x���ʵ�ȡֵ������(����)
(a>0��b>0)�����ҽ��c(di��n)���^F1�Ҵ�ֱ��x�S��ֱ���c�p��������A��B���c(di��n)������ABF2���J�������Σ��tԓ�p�����x���ʵ�ȡֵ������(����)A��(1�� ) ) | B��( ��2 ��2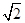 ) ) |
C��(1��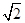 ������) ������) | D��(1,1��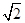 ) ) |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
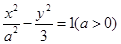 ���x���ʞ�2���t
���x���ʞ�2���t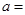
| A��2 | B��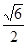 | C��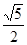 | D��1 |
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com