
【題目】若函數![]() 的導函數
的導函數![]() ,
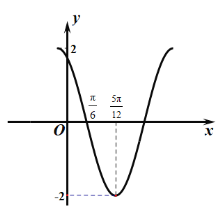
,![]() 的部分圖象如圖所示,
的部分圖象如圖所示,![]() ,當
,當![]() ,
,![]() 時,則
時,則![]() 的最大值為_________.
的最大值為_________.
【答案】![]()
【解析】
由圖象可得:A=2,![]() ,解得ω=2.可得f′(x)=2cos(2
,解得ω=2.可得f′(x)=2cos(2![]() φ)=﹣2,|φ|
φ)=﹣2,|φ|![]() ),把x
),把x![]() ,
,![]() 2代入解得φ.可得f′(x),進而得出f(x),g(x)=f(x
2代入解得φ.可得f′(x),進而得出f(x),g(x)=f(x![]() ),利用正弦函數的單調性即可得出結論.
),利用正弦函數的單調性即可得出結論.
由圖象可得:A=2,![]() ,解得ω=2.
,解得ω=2.
∴f′(x)=2cos(2![]() φ)=﹣2,|φ|
φ)=﹣2,|φ|![]() ),解得φ
),解得φ![]() .
.
∴f′(x)=2cos(2x![]() ).
).
∴f(x)=sin(2x![]() )+c.(c為常數).
)+c.(c為常數).
g(x)=f(x![]() )=sin2x+c.
)=sin2x+c.
x∈[![]() ,
,![]() ]時,2x∈
]時,2x∈![]() .
.
sin2x∈![]() ,
,
當x1,x2∈[![]() ,
,![]() ]時,則|g(x1)﹣g(x2)|=|sin2x1﹣sin2x2|≤1﹣(
]時,則|g(x1)﹣g(x2)|=|sin2x1﹣sin2x2|≤1﹣(![]() )
)![]() .
.
因此當x1,x2∈[![]() ,
,![]() ]時,則|g(x1)﹣g(x2)|的最大值為
]時,則|g(x1)﹣g(x2)|的最大值為![]() .
.
故答案為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若對![]() 時,不等式
時,不等式![]() 恒成立,求實數a的取值范圍(e為自然對數的底數);
恒成立,求實數a的取值范圍(e為自然對數的底數);
(2)當![]() 時,求函數
時,求函數![]() 的極大值;
的極大值;
(3)求證:當![]() 時,曲線
時,曲線![]() 與直線
與直線![]() 有且僅有一個公共點.
有且僅有一個公共點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過原點![]() 的動直線
的動直線![]() 與圓
與圓![]() :
: ![]() 交于
交于![]() 兩點.
兩點.
(1)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得當
,使得當![]() 變動時,總有直線
變動時,總有直線![]() 的斜率之和為0?若存在,求出
的斜率之和為0?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,底面
,底面![]() 是平行四邊形,
是平行四邊形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中點,點
中點,點![]() 在線段
在線段![]() 上.
上.
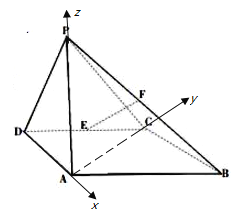
(Ⅰ)證明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求實數
,求實數![]() 使直線
使直線![]() 與平面
與平面![]() 所成角和直線
所成角和直線![]() 與平面
與平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一種擲骰子走跳棋的游戲:棋盤上標有第0站、第1站、第2站、…、第100站,共101站,設棋子跳到第n站的概率為![]() ,一枚棋子開始在第0站,棋手每擲一次骰子,棋子向前跳動一次.若擲出奇數點,棋子向前跳一站;若擲出偶數點,棋子向前跳兩站,直到棋子跳到第99站(獲勝)或第100站(失敗)時,游戲結束(骰子是用一種均勻材料做成的立方體形狀的游戲玩具,它的六個面分別標有點數1,2,3,4,5,6).
,一枚棋子開始在第0站,棋手每擲一次骰子,棋子向前跳動一次.若擲出奇數點,棋子向前跳一站;若擲出偶數點,棋子向前跳兩站,直到棋子跳到第99站(獲勝)或第100站(失敗)時,游戲結束(骰子是用一種均勻材料做成的立方體形狀的游戲玩具,它的六個面分別標有點數1,2,3,4,5,6).
(1)求![]() ,
,![]() ,
,![]() ,并根據棋子跳到第n站的情況,試用
,并根據棋子跳到第n站的情況,試用![]() 和
和![]() 表示
表示![]() ;
;
(2)求證:![]() 為等比數列;
為等比數列;
(3)求玩該游戲獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖,90后從事互聯網行業崗位分布條形圖,則下列結論中不正確的是( )
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.


A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的![]()
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省新課改后某校為預測2020屆高三畢業班的本科上線情況,從該校上一屆高三(1)班到高三(5)班隨機抽取50人,得到各班抽取的人數和其中本科上線人數,并將抽取數據制成下面的條形統計圖.

(1)根據條形統計圖,估計本屆高三學生本科上線率.
(2)已知該省甲市2020屆高考考生人數為4萬,假設以(1)中的本科上線率作為甲市每個考生本科上線的概率.
(i)若從甲市隨機抽取10名高三學生,求恰有8名學生達到本科線的概率(結果精確到0.01);
(ii)已知該省乙市2020屆高考考生人數為3.6萬,假設該市每個考生本科上線率均為![]() ,若2020屆高考本科上線人數乙市的均值不低于甲市,求p的取值范圍.
,若2020屆高考本科上線人數乙市的均值不低于甲市,求p的取值范圍.
可能用到的參考數據:取![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com