
分析 根據拋物線方程可表示出焦點F的坐標,進而求得B點的坐標代入拋物線方程求得p,則B點坐標和拋物線準線方程可求,進而求得B到該拋物線準線的距離.
解答 解:依題意可知F坐標為($\frac{p}{2}$,0)
∴B的坐標為($\frac{p}{4}$,-1)代入拋物線方程得$\frac{{p}^{2}}{2}$=1,解得p=$\sqrt{2}$,
∴拋物線準線方程為x=-$\frac{\sqrt{2}}{2}$
所以點B到拋物線準線的距離為$\frac{\sqrt{2}}{4}$+$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{4}$,
故答案為:$\frac{3\sqrt{2}}{4}$.
點評 本題主要考查拋物線的定義及幾何性質,考查計算能力.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
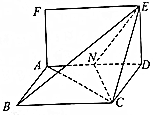 已知矩形ADEF和菱形ABCD所在平面互相垂直,如圖,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,點N時線段AD的中點.
已知矩形ADEF和菱形ABCD所在平面互相垂直,如圖,其中AF=1,AD=2,∠ADC=$\frac{π}{3}$,點N時線段AD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com