Question

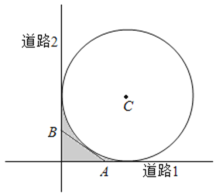
【題目】如圖，某城市有一塊半徑為（單位：百米）的圓形景觀，圓心為，有兩條與圓形景觀相切且互相垂直的道路.最初規劃在拐角處圖中陰影部分只有一塊綠化地，后來有眾多市民建議在綠化地上建一條小路，便于市民快捷地往返兩條道路.規劃部門采納了此建議，決定在綠化地中增建一條與圓相切的小道問：兩點應選在何處可使得小道最短？

Answer 1

【答案】當兩點離道路的交點都為（百米）時，小道最短

【解析】

分別由兩條道路所在直線建立直角坐標系，設，，求得直線的方程和圓的方程，運用直線和圓相切的條件：，求得的關系，再由兩點的距離公式和基本不等式，解不等式可得的最小值，以及此時的位置.

解：如圖，分別由兩條道路所在直線建立直角坐標系xOy.

設，，

則直線方程為，即.

因為與圓相切，所以

化簡得，即

因此

因為，，所以

于是

又

解得，或

因為，所以

所以

當且僅當時取等號

所以最小值為，此時

答：當兩點離道路的交點都為（百米）時，小道最短