
【題目】已知函數(shù)![]() .
.
(1)若![]() ,且函數(shù)
,且函數(shù)![]() 在其定義域內(nèi)為增函數(shù),求實(shí)數(shù)
在其定義域內(nèi)為增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)函數(shù)![]() ,若在
,若在![]() 上至少存在一點(diǎn)
上至少存在一點(diǎn)![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)![]() =
=![]() ,求其導(dǎo)函數(shù),利用F(x)在定義域(0,+∞)內(nèi)為增函數(shù),得
,求其導(dǎo)函數(shù),利用F(x)在定義域(0,+∞)內(nèi)為增函數(shù),得![]() ≥0在(0,+∞)上恒成立,得
≥0在(0,+∞)上恒成立,得![]() ,設(shè)
,設(shè)![]() ,利用導(dǎo)數(shù)求
,利用導(dǎo)數(shù)求![]() 最大值可得正實(shí)數(shù)p的取值范圍;
最大值可得正實(shí)數(shù)p的取值范圍;
(2)設(shè)函數(shù)![]() =f(x)﹣g(x)=px﹣
=f(x)﹣g(x)=px﹣![]() ,x∈[1,e],轉(zhuǎn)化為
,x∈[1,e],轉(zhuǎn)化為![]() 在[1,e]上至少存在一點(diǎn)x0,使得
在[1,e]上至少存在一點(diǎn)x0,使得![]() 求函數(shù)
求函數(shù)![]() 的導(dǎo)函數(shù),然后對(duì)p分類(lèi)求
的導(dǎo)函數(shù),然后對(duì)p分類(lèi)求![]() 的最大值即可.
的最大值即可.
(1)![]() ,
,![]() .
.
由![]() 定義域
定義域![]() 內(nèi)為增函數(shù),所以
內(nèi)為增函數(shù),所以![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 即
即![]() ,對(duì)任意
,對(duì)任意![]() 恒成立,
恒成立,
設(shè)![]() ,
,![]() =0的根為x=1
=0的根為x=1
得![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
則![]() ,所以
,所以![]() ,即
,即![]() .
.
(2)設(shè)函數(shù)![]() ,
,![]() ,
,
因?yàn)樵?/span>![]() 上至少存在一點(diǎn)
上至少存在一點(diǎn)![]() ,使得
,使得![]() 成立,則
成立,則![]()
![]() ,
,
①當(dāng)![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() ,舍;
,舍;
②當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,則
,則![]() ,舍;
,舍;
③當(dāng)![]() 時(shí),
時(shí),![]() ,
,
則![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() ,得
,得![]() ,
,
綜上,![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的最小值;
的最小值;
(2)若![]() 時(shí),
時(shí),![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】黨的“十八大”之后,做好農(nóng)業(yè)農(nóng)村工作具有特殊重要的意義.國(guó)家為了更 好地服務(wù)于農(nóng)民、開(kāi)展社會(huì)主義新農(nóng)村工作,派調(diào)查組到農(nóng)村某地區(qū)考察.該地區(qū)有100戶(hù)農(nóng) 民,且都從事蔬菜種植.據(jù)了解,平均每戶(hù)的年收入為6萬(wàn)元.為了調(diào)整產(chǎn)業(yè)結(jié)構(gòu),當(dāng)?shù)卣疀Q 定動(dòng)員部分農(nóng)民從事蔬菜加工.據(jù)統(tǒng)計(jì),若動(dòng)員![]() 戶(hù)農(nóng)民從事蔬菜加工,則剩下的繼續(xù) 從事蔬菜種植的農(nóng)民平均每戶(hù)的年收入有望提高
戶(hù)農(nóng)民從事蔬菜加工,則剩下的繼續(xù) 從事蔬菜種植的農(nóng)民平均每戶(hù)的年收入有望提高![]() ,而從事蔬菜加工的農(nóng)民平均每戶(hù)的年收入為
,而從事蔬菜加工的農(nóng)民平均每戶(hù)的年收入為![]() 萬(wàn)元.
萬(wàn)元.
(1)在動(dòng)員![]() 戶(hù)農(nóng)民從事蔬菜加工后,要使剩下
戶(hù)農(nóng)民從事蔬菜加工后,要使剩下![]() 戶(hù)從事蔬菜種植的所有農(nóng)民總年收 入不低于動(dòng)員前100戶(hù)從事蔬菜種植的所有農(nóng)民年總年收入,求
戶(hù)從事蔬菜種植的所有農(nóng)民總年收 入不低于動(dòng)員前100戶(hù)從事蔬菜種植的所有農(nóng)民年總年收入,求![]() 的取值范圍;
的取值范圍;
(2)在(1)的條件下,要使這![]() 戶(hù)農(nóng)民從事蔬菜加工的總年收入始終不高于
戶(hù)農(nóng)民從事蔬菜加工的總年收入始終不高于![]() 戶(hù)從事蔬菜種植的所有農(nóng)民年總年收入,求
戶(hù)從事蔬菜種植的所有農(nóng)民年總年收入,求![]() 的最大值.(參考數(shù)據(jù):
的最大值.(參考數(shù)據(jù):![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示的五個(gè)區(qū)域中,中心區(qū)![]() 域是一幅圖畫(huà),現(xiàn)要求在其余四個(gè)區(qū)域中涂色,有四種顏色可供選擇.要求每個(gè)區(qū)域只涂一種顏色且相鄰區(qū)域所涂顏色不同,則不同的涂色方法種數(shù)為( )
域是一幅圖畫(huà),現(xiàn)要求在其余四個(gè)區(qū)域中涂色,有四種顏色可供選擇.要求每個(gè)區(qū)域只涂一種顏色且相鄰區(qū)域所涂顏色不同,則不同的涂色方法種數(shù)為( )

A. 56 B. 72 C. 64 D. 84
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
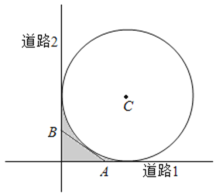
【題目】如圖,某城市有一塊半徑為![]() (單位:百米)的圓形景觀,圓心為
(單位:百米)的圓形景觀,圓心為![]() ,有兩條與圓形景觀相切且互相垂直的道路.最初規(guī)劃在拐角處
,有兩條與圓形景觀相切且互相垂直的道路.最初規(guī)劃在拐角處![]() 圖中陰影部分
圖中陰影部分![]() 只有一塊綠化地,后來(lái)有眾多市民建議在綠化地上建一條小路,便于市民快捷地往返兩條道路.規(guī)劃部門(mén)采納了此建議,決定在綠化地中增建一條與圓
只有一塊綠化地,后來(lái)有眾多市民建議在綠化地上建一條小路,便于市民快捷地往返兩條道路.規(guī)劃部門(mén)采納了此建議,決定在綠化地中增建一條與圓![]() 相切的小道
相切的小道![]() 問(wèn):
問(wèn):![]() 兩點(diǎn)應(yīng)選在何處可使得小道
兩點(diǎn)應(yīng)選在何處可使得小道![]() 最短?
最短?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某醫(yī)院治療白血病有甲、乙兩套方案,現(xiàn)就70名患者治療后復(fù)發(fā)的情況進(jìn)行了統(tǒng)計(jì),得到其等高條形圖如圖所示(其中采用甲、乙兩種治療方案的患者人數(shù)之比為![]() ).
).
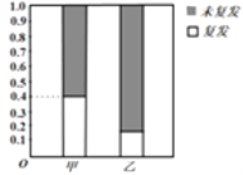
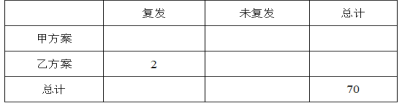
(1)補(bǔ)充完整![]() 列聯(lián)表中的數(shù)據(jù),并判斷是否有
列聯(lián)表中的數(shù)據(jù),并判斷是否有![]() 的把握認(rèn)為甲、乙兩套治療方案對(duì)患者白血病復(fù)發(fā)有影響;
的把握認(rèn)為甲、乙兩套治療方案對(duì)患者白血病復(fù)發(fā)有影響;
(2)從復(fù)發(fā)的患者中抽取3人進(jìn)行分析,求其中接受“乙方案”治療的人數(shù)![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
附:
|
|
|
|
|
|
|
|
|
|
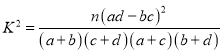 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】關(guān)于![]() 的說(shuō)法,錯(cuò)誤的是( )
的說(shuō)法,錯(cuò)誤的是( )
A.展開(kāi)式中的二項(xiàng)式系數(shù)之和為1024
B.展開(kāi)式中第6項(xiàng)的二項(xiàng)式系數(shù)最大
C.展開(kāi)式中第5項(xiàng)和第7項(xiàng)的二項(xiàng)式系數(shù)最大
D.展開(kāi)式中第6項(xiàng)的系數(shù)最小
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() .討論函數(shù)
.討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)證明當(dāng)![]() .
.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com