
【題目】已知函數![]() ,函數
,函數![]() .
.
(1)討論函數![]() 的極值;
的極值;
(2)已知函數![]() ,若函數
,若函數![]() 在
在![]() 上恰有三個零點,求實數
上恰有三個零點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】
(1)對![]() 求導,分
求導,分![]() 和
和![]() 兩種情況,分別討論
兩種情況,分別討論![]() 的正負性,可得到
的正負性,可得到![]() 的單調性,進而可求得極值;
的單調性,進而可求得極值;
(2)易知![]() 有且僅有一個零點
有且僅有一個零點![]() ,且
,且![]() 時
時![]() ,從而可知
,從而可知![]() 有兩個零點,結合(1)知
有兩個零點,結合(1)知![]() 不符合題意,
不符合題意,![]() 時,討論
時,討論![]() 的極值,并結合零點存在性定理可求出答案.
的極值,并結合零點存在性定理可求出答案.
(1)![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
當![]() 時,
時,![]() 在
在![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 單調遞減,故
單調遞減,故![]() 無極值,
無極值,
當![]() 時,由
時,由![]() 得
得![]() .
.
當![]() 時,
時,![]() ,則
,則![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,則
,則![]() 單調遞增,
單調遞增,
∴![]() 在
在![]() 處取得極小值,
處取得極小值,![]() ,
,![]() 無極大值.
無極大值.
綜上,當![]() 時,
時,![]() 無極值;當
無極值;當![]() 時,
時,![]() 有極小值
有極小值![]() ,無極大值.
,無極大值.
(2)若![]() 是
是![]() 的零點,則必有
的零點,則必有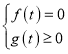 或
或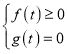 ,∴
,∴![]() 的零點必為
的零點必為![]() 或
或![]() 的零點,
的零點,
而![]() 有且僅有一個零點
有且僅有一個零點![]() ,且
,且![]() ,
,![]() 時
時![]() .
.
①當![]() 時,由(1)知
時,由(1)知![]() 在
在![]() 單調遞減,至多只有一個零點,此時
單調遞減,至多只有一個零點,此時![]() 至多只有兩個零點,不合題意,舍去;
至多只有兩個零點,不合題意,舍去;
②當![]() 時,由(1)知
時,由(1)知![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,則
單調遞增,則![]() .
.
i)當![]() 即
即![]() 時,
時,![]() 至多只有一個零點
至多只有一個零點![]() ,此時
,此時![]() 至多只有兩個零點,不合題意,舍去;
至多只有兩個零點,不合題意,舍去;
ii)當![]() 即
即![]() 時,
時,![]() ,
,![]() ,
,
由零點存在性定理知![]() 使得
使得![]() .
.
令![]() ,
,![]() ,則
,則![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,
單調遞減,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,
∴![]() ,又
,又![]() ,
,
∴由零點存在性定理知![]() 使得
使得![]() ,
,
∴![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ,
,
∴當![]() 時,
時,![]() 有三個零點,滿足題意.
有三個零點,滿足題意.
綜上,實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】某種子公司對一種新品種的種子的發芽多少與晝夜溫差之間的關系進行分析研究,以便選擇最合適的種植條件.他們分別記錄了10塊試驗地每天的晝夜溫差和每塊實驗地里50顆種子的發芽數,得到如下資料:

(1)從上述十組試驗數據來看,是否可以判斷晝夜溫差與發芽數之間具有相關關系?是否具有線性相關關系?
(2)若在一定溫度范圍內,晝夜溫差與發芽數近似滿足相關關系:![]() (其中
(其中![]() ).取后五組數據,利用最小二乘法求出線性回歸方程
).取后五組數據,利用最小二乘法求出線性回歸方程![]() (精確到0.01);
(精確到0.01);
(3)利用(2)的結論,若發芽數試驗值與預測值差的絕對值不超過3個就認為正常,否則認為不正常.從上述十組試驗中任取三組,至少有兩組正常的概率是多少?
附:回歸直線方程![]() 的斜率和截距的最小二乘估計公式分別為
的斜率和截距的最小二乘估計公式分別為 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的“十八大”之后,做好農業農村工作具有特殊重要的意義.國家為了更 好地服務于農民、開展社會主義新農村工作,派調查組到農村某地區考察.該地區有100戶農 民,且都從事蔬菜種植.據了解,平均每戶的年收入為6萬元.為了調整產業結構,當地政府決 定動員部分農民從事蔬菜加工.據統計,若動員![]() 戶農民從事蔬菜加工,則剩下的繼續 從事蔬菜種植的農民平均每戶的年收入有望提高
戶農民從事蔬菜加工,則剩下的繼續 從事蔬菜種植的農民平均每戶的年收入有望提高![]() ,而從事蔬菜加工的農民平均每戶的年收入為
,而從事蔬菜加工的農民平均每戶的年收入為![]() 萬元.
萬元.
(1)在動員![]() 戶農民從事蔬菜加工后,要使剩下
戶農民從事蔬菜加工后,要使剩下![]() 戶從事蔬菜種植的所有農民總年收 入不低于動員前100戶從事蔬菜種植的所有農民年總年收入,求
戶從事蔬菜種植的所有農民總年收 入不低于動員前100戶從事蔬菜種植的所有農民年總年收入,求![]() 的取值范圍;
的取值范圍;
(2)在(1)的條件下,要使這![]() 戶農民從事蔬菜加工的總年收入始終不高于
戶農民從事蔬菜加工的總年收入始終不高于![]() 戶從事蔬菜種植的所有農民年總年收入,求
戶從事蔬菜種植的所有農民年總年收入,求![]() 的最大值.(參考數據:
的最大值.(參考數據:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果存在常數![]() ,使得數列
,使得數列![]() 滿足:若
滿足:若![]() 是數列
是數列![]() 中的一項,則
中的一項,則![]() 也是數列
也是數列![]() 中的一項,稱數列
中的一項,稱數列![]() 為“兌換數列”,常數
為“兌換數列”,常數![]() 是它的“兌換系數”.
是它的“兌換系數”.
(1)若數列:![]()
![]() 是“兌換系數”為
是“兌換系數”為![]() 的“兌換數列”,求
的“兌換數列”,求![]() 和
和![]() 的值;
的值;
(2)已知有窮等差數列![]() 的項數是
的項數是![]()
![]() ,所有項之和是
,所有項之和是![]() ,求證:數列
,求證:數列![]() 是“兌換數列”,并用
是“兌換數列”,并用![]() 和
和![]() 表示它的“兌換系數”;
表示它的“兌換系數”;
(3)對于一個不小于3項,且各項皆為正整數的遞增數列![]() ,是否有可能它既是等比數列,又是“兌換數列”?給出你的結論,并說明理由.
,是否有可能它既是等比數列,又是“兌換數列”?給出你的結論,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
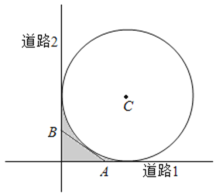
【題目】如圖,某城市有一塊半徑為![]() (單位:百米)的圓形景觀,圓心為
(單位:百米)的圓形景觀,圓心為![]() ,有兩條與圓形景觀相切且互相垂直的道路.最初規劃在拐角處
,有兩條與圓形景觀相切且互相垂直的道路.最初規劃在拐角處![]() 圖中陰影部分
圖中陰影部分![]() 只有一塊綠化地,后來有眾多市民建議在綠化地上建一條小路,便于市民快捷地往返兩條道路.規劃部門采納了此建議,決定在綠化地中增建一條與圓
只有一塊綠化地,后來有眾多市民建議在綠化地上建一條小路,便于市民快捷地往返兩條道路.規劃部門采納了此建議,決定在綠化地中增建一條與圓![]() 相切的小道
相切的小道![]() 問:
問:![]() 兩點應選在何處可使得小道
兩點應選在何處可使得小道![]() 最短?
最短?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一點.
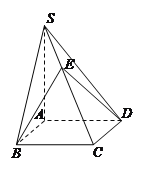
(1)求證:平面EBD⊥平面SAC;
(2)設SA=4,AB=2,求點A到平面SBD的距離;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 過點
過點![]() ,且離心率為
,且離心率為![]()
(Ⅰ)求橢圓C的方程;
(Ⅱ)若過原點的直線![]() 與橢圓C交于P、Q兩點,且在直線
與橢圓C交于P、Q兩點,且在直線![]() 上存在點M,使得
上存在點M,使得![]() 為等邊三角形,求直線
為等邊三角形,求直線![]() 的方程。
的方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com