
【題目】已知![]() .
.
(1)設![]() 是
是![]() 的極值點,求實數
的極值點,求實數![]() 的值,并求
的值,并求![]() 的單調區間:
的單調區間:
(2)![]() 時,求證:
時,求證:![]() .
.
【答案】(1)![]() 單調遞增區間為
單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ; (2)見解析.
; (2)見解析.
【解析】
(1)由題意,求得函數的導數![]() ,由
,由![]() 是函數
是函數![]() 的極值點,解得
的極值點,解得![]() ,又由
,又由![]() ,進而得到函數的單調區間;
,進而得到函數的單調區間;
(2)由(1),進而得到函數![]() 的單調性和最小值
的單調性和最小值![]() ,令
,令![]() ,利用導數求得
,利用導數求得![]() 在
在![]() 上的單調性,即可作出證明.
上的單調性,即可作出證明.
(1)由題意,函數![]() 的定義域為
的定義域為![]() ,
,
又由![]() ,且
,且![]() 是函數
是函數![]() 的極值點,
的極值點,
所以![]() ,解得
,解得![]() ,
,
又![]() 時,在
時,在![]() 上,
上,![]() 是增函數,且
是增函數,且![]() ,
,
所以![]() ,得
,得![]() ,
,![]() ,得
,得![]() ,
,
所以函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(2)由(1)知因為![]() ,在
,在![]() 上,
上,![]() 是增函數,
是增函數,
又![]() (且當自變量
(且當自變量![]() 逐漸趨向于
逐漸趨向于![]() 時,
時,![]() 趨向于
趨向于![]() ),
),
所以,![]() ,使得
,使得![]() ,
,
所以![]() ,即
,即![]() ,
,
在![]() 上,
上,![]() ,函數
,函數![]() 是減函數,
是減函數,
在![]() 上,
上,![]() ,函數
,函數![]() 是增函數,
是增函數,
所以,當![]() 時,
時,![]() 取得極小值,也是最小值,
取得極小值,也是最小值,
所以![]() ,
,
令![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減,所以
單調遞減,所以![]() ,
,
即![]() 成立,
成立,


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直線AB,且AB![]() BP
BP![]() 2,AD=AE=1,AE⊥AB,且AE∥BP.
2,AD=AE=1,AE⊥AB,且AE∥BP.

(1)求平面PCD與平面ABPE所成的二面角的余弦值;
(2)線段PD上是否存在一點N,使得直線BN與平面PCD所成角的正弦值等于![]() ?若存在,試確定點N的位置;若不存在,請說明理由.
?若存在,試確定點N的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,橢圓E:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,焦距為2.
,焦距為2.

(1)求橢圓E的方程;
(2)如圖,動直線l:y=k1x-![]() 交橢圓E于A,B兩點,C是橢圓E上一點,直線OC的斜率為k2,且k1k2=
交橢圓E于A,B兩點,C是橢圓E上一點,直線OC的斜率為k2,且k1k2=![]() .M是線段OC延長線上一點,且|MC|∶|AB|=2∶3,⊙M的半徑為|MC|,OS,OT是⊙M的兩條切線,切點分別為S,T.求∠SOT的最大值,并求取得最大值時直線l的斜率.
.M是線段OC延長線上一點,且|MC|∶|AB|=2∶3,⊙M的半徑為|MC|,OS,OT是⊙M的兩條切線,切點分別為S,T.求∠SOT的最大值,并求取得最大值時直線l的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,直線l的參數方程為![]() (t為參數,0).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數,0).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() .
.
(Ⅰ)寫出曲線C的直角坐標方程;
(Ⅱ)若直線l與曲線C交于A,B兩點,且AB的長度為2![]() ,求直線l的普通方程.
,求直線l的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(x1,f(x1)),B(x2,f(x2))是函數f(x)=2sin(ωx+φ)![]() 圖象上的任意兩點,且角φ的終邊經過點
圖象上的任意兩點,且角φ的終邊經過點![]() ,若|f(x1)﹣f(x2)|=4時,|x1﹣x2|的最小值為
,若|f(x1)﹣f(x2)|=4時,|x1﹣x2|的最小值為![]() .
.
(1)求函數f(x)的解析式;
(2)求函數f(x)的單調遞增區間;
(3)當![]() 時,不等式mf(x)+2m≥f(x)恒成立,求實數m的取值范圍.
時,不等式mf(x)+2m≥f(x)恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,OB、CD是兩條互相平行的筆直公路,且均與筆直公路OC垂直(公路寬度忽略不計),半徑OC=1千米的扇形COA為該市某一景點區域,當地政府為緩解景點周邊的交通壓力,欲在圓弧AC上新增一個入口E(點E不與A、C重合),并在E點建一段與圓弧相切(E為切點)的筆直公路與OB、CD分別交于M、N.當公路建成后,計劃將所圍成的區域在景點之外的部分建成停車場(圖中陰影部分),設∠CON=θ,停車場面積為S平方千米.
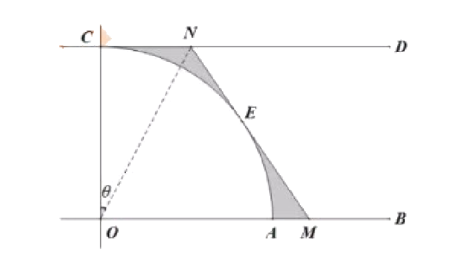
(1)求函數S=f(θ)的解析式,并寫出函數的定義域;
(2)為對該計劃進行可行性研究,需要預知所建停車場至少有多少面積,請計算當θ為何值時,S有最小值,并求出該最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱臺![]() 的上下底面分別是邊長為2和4的正方形,
的上下底面分別是邊長為2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
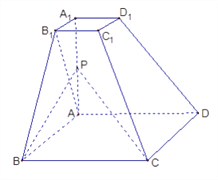
(Ⅰ)求證: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 邊上找一點
邊上找一點![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com