
分析 根據平面向量的數量積運算性質計算$\overrightarrow{a}•\overrightarrow{b}$,得出cos<$\overrightarrow{a},\overrightarrow{b}$>,再代入投影公式計算.
解答 解:∵${\overrightarrow{a}}^{2}$=4,$\overrightarrow{a}$($\overrightarrow{b}-\overrightarrow{a}$)=$\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{a}}^{2}$=-3,
∴$\overrightarrow{a}•\overrightarrow{b}$=1,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{2|\overrightarrow{b}|}$,
∴$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影為|$\overrightarrow{b}$|cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{1}{2}$.
故答案為:$\frac{1}{2}$.
點評 本題考查了平面向量的數量積運算,屬于基礎題.


 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:解答題
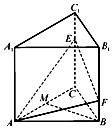 三棱柱ABC-A1B1C1的底面是邊長為2的正三角形,側棱A1A⊥底面ABC,點E,F分別是棱CC1,BB1上的點,點M是線段AC上的動點,EC=2FB=2.
三棱柱ABC-A1B1C1的底面是邊長為2的正三角形,側棱A1A⊥底面ABC,點E,F分別是棱CC1,BB1上的點,點M是線段AC上的動點,EC=2FB=2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 一解 | B. | 二解 | C. | 無解 | D. | 不能確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,+∞) | B. | (-1,1) | C. | [-1,1] | D. | (-∞,1] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com