
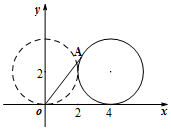
 如圖,半徑為2的圓圓心的初始位置坐標為(0,2),圓上一點A坐標為(0,0).圓沿x軸正向滾動,當圓滾動到圓心位于(4,2)時,A點坐標為(4-2sin2,2-2cos2).
如圖,半徑為2的圓圓心的初始位置坐標為(0,2),圓上一點A坐標為(0,0).圓沿x軸正向滾動,當圓滾動到圓心位于(4,2)時,A點坐標為(4-2sin2,2-2cos2). 分析 設滾動后的圓的圓心為O',切點為C(4,0),連接O'A,過O'作與x軸正方向平行的射線,交圓O'于B(6,2),設∠BO'A=θ,則根據圓的參數方程,得P的坐標,再根據圓的圓心從(0,2)滾動到(4,2),算出θ,結合三角函數的誘導公式,化簡可得A的坐標.
解答 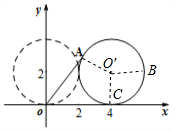 解:設滾動后的圓的圓心為O',切點為C(4,0),連接O'A,
解:設滾動后的圓的圓心為O',切點為C(4,0),連接O'A,
過O'作與x軸正方向平行的射線,交圓O'于B(6,2),設∠BO'A=θ,
∵⊙O'的方程為(x-4)2+(y-2)2=4,
∴根據圓的參數方程,得A的坐標為(4+2cosθ,2+2sinθ),
∵單位圓的圓心的初始位置在(0,2),圓滾動到圓心位于(4,2)
∴可得θ=$\frac{3π}{2}$-2
可得cosθ=cos($\frac{3π}{2}$-2)=-sin2,sinθ=sin($\frac{3π}{2}$-2)=-cos2,
代入上面所得的式子,得到A的坐標為(4-2sin2,2-2cos2).
故答案為(4-2sin2,2-2cos2)
點評 本題根據半徑為2的圓的滾動,求一個向量的坐標,著重考查了圓的參數方程和平面向量的坐標表示的應用等知識點,屬于中檔題.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | ∅ | B. | [-1,0) | C. | $[1,\frac{9}{2}]$ | D. | [0,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 0 | C. | π | D. | π+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{2b}{a}$ | B. | $-\frac{2a}{b}$ | C. | $-\frac{{\sqrt{2}b}}{a}$ | D. | $-\frac{{\sqrt{2}b}}{a}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (8,9) | B. | (9,10) | C. | (10,11) | D. | (11,12) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com