
【題目】某學校為了了解高一年級學生學習數(shù)學的狀態(tài),從期中考試成績中隨機抽取50名學生的數(shù)學成績,按成績分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
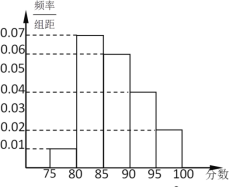
(1)由頻率分布直方圖,估計這50名學生數(shù)學成績的中位數(shù)和平均數(shù)(保留到0.01);
(2)該校高一年級共有1000名學生,若本次考試成績90分以上(含90分)為“優(yōu)秀”等次,則根據(jù)頻率分布直方圖估計該校高一學生數(shù)學成績達到“優(yōu)秀”等次的人數(shù).
【答案】(1)中位數(shù)為![]() ,平均數(shù)為
,平均數(shù)為![]() (2)
(2)![]()
【解析】
(1)設這50名學生數(shù)學成績的中位數(shù)和平均數(shù)分別為![]() ,因為前2組的頻率之和為
,因為前2組的頻率之和為![]() ,因為前3組的頻率之和為
,因為前3組的頻率之和為![]() ,所以
,所以![]() ,求出
,求出![]() 即可求得答案;
即可求得答案;
(2)因為樣本中90分及以上的頻率為![]() ,所以該校高一年級1000名學生中,根據(jù)頻率分布直方圖,即可估計該校高一學生數(shù)學成績達到人數(shù).
,所以該校高一年級1000名學生中,根據(jù)頻率分布直方圖,即可估計該校高一學生數(shù)學成績達到人數(shù).
“優(yōu)秀”等次的人數(shù)
(1)設這50名學生數(shù)學成績的中位數(shù)和平均數(shù)分別為![]()
因為前2組的頻率之和為![]() ,因為前3組的頻率之和為
,因為前3組的頻率之和為![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() .
.
![]() 所以,這50名學生數(shù)學成績的中位數(shù)和平均數(shù)分別為
所以,這50名學生數(shù)學成績的中位數(shù)和平均數(shù)分別為![]() ,
,![]()
(2)因為樣本中90分及以上的頻率為![]() ,
,
所以該校高一年級1000名學生中,根據(jù)頻率分布直方圖估計該校高一學生數(shù)學成績達到
“優(yōu)秀”等次的人數(shù)為![]() 人.
人.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】“搜索指數(shù)”是網(wǎng)民通過搜索引擎,以每天搜索關鍵詞的次數(shù)為基礎所得到的統(tǒng)計指標.“搜索指數(shù)”越大,表示網(wǎng)民對該關鍵詞的搜索次數(shù)越多,對該關鍵詞相關的信息關注度也越高.下圖是2017年9月到2018年2月這半年中,某個關鍵詞的搜索指數(shù)變化的走勢圖.

根據(jù)該走勢圖,下列結論正確的是( )
A. 這半年中,網(wǎng)民對該關鍵詞相關的信息關注度呈周期性變化
B. 這半年中,網(wǎng)民對該關鍵詞相關的信息關注度不斷減弱
C. 從網(wǎng)民對該關鍵詞的搜索指數(shù)來看,去年10月份的方差小于11月份的方差
D. 從網(wǎng)民對該關鍵詞的搜索指數(shù)來看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖:已知四棱錐P—ABCD的底面ABCD是平行四邊形,PA⊥面ABCD,M是AD的中點,N是PC的中點.

(1)求證:MN∥面PAB;
(2)若平面PMC⊥面PAD,求證:CM⊥AD.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若函數(shù)![]() 與
與![]() 的圖象上存在關于原點對稱的點,求實數(shù)
的圖象上存在關于原點對稱的點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設![]() ,已知
,已知![]() 在
在![]() 上存在兩個極值點
上存在兩個極值點![]() ,
,![]() ,且
,且![]() ,求證:
,求證:![]() (其中
(其中![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1所示,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 中點,將
中點,將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到點
到點![]() 處,且平面
處,且平面![]() 平面
平面![]() ,如圖2所示.
,如圖2所示.
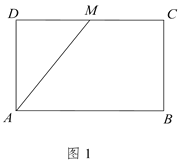
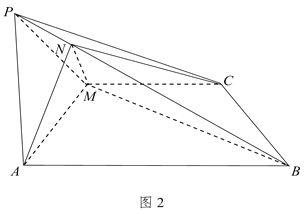
(1)求證:![]() :
:
(2)在棱![]() 上取點
上取點![]() ,使平面
,使平面![]() 平面
平面![]() ,求平面
,求平面![]() 與
與![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年來,隨著網(wǎng)絡的普及,數(shù)碼產(chǎn)品早已走進千家萬戶的生活,為了節(jié)約資源,促進資源循環(huán)利用,折舊產(chǎn)品回收行業(yè)得到迅猛發(fā)展,電腦使用時間越長,回收價值越低,某二手電腦交易市場對2018年回收的折舊電腦交易前使用的時間進行了統(tǒng)計,得到如圖所示的頻率分布直方圖,在如圖對時間使用的分組中,將使用時間落入各組的頻率視為概率.
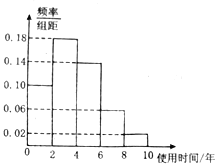
(1)若在該市場隨機選取1個2018年成交的二手電腦,求其使用時間在![]() 上的概率;
上的概率;
(2)根據(jù)電腦交易市場往年的數(shù)據(jù),得到如圖所示的散點圖及一些統(tǒng)計量的值,其中![]() (單位:年)表示折舊電腦的使用時間,
(單位:年)表示折舊電腦的使用時間,![]() (單位:百元)表示相應的折舊電腦的平均交易價格.
(單位:百元)表示相應的折舊電腦的平均交易價格.
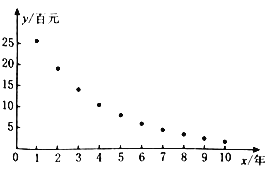
由散點圖判斷,可采用![]() 作為該交易市場折舊電腦平均交易價格與使用年限
作為該交易市場折舊電腦平均交易價格與使用年限![]() 的回歸方程,若
的回歸方程,若![]() ,
,![]() ,選用如下參考數(shù)據(jù),求
,選用如下參考數(shù)據(jù),求![]() 關于
關于![]() 的回歸方程,并預測在區(qū)間
的回歸方程,并預測在區(qū)間![]() (用時間組的區(qū)間中點值代表該組的值)上折舊電腦的價格.
(用時間組的區(qū)間中點值代表該組的值)上折舊電腦的價格.
|
|
|
|
|
|
5.5 | 8.5 | 1.9 | 301.4 | 79.75 | 385 |
附:參考公式:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: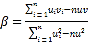 ,
,![]() .參考數(shù)據(jù):
.參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .(
.(![]() 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
(1)設![]() ;
;
①若函數(shù)![]() 在
在![]() 處的切線過點
處的切線過點![]() ,求
,求![]() 的值;
的值;
②當![]() 時,若函數(shù)
時,若函數(shù)![]() 在
在![]() 上沒有零點,求
上沒有零點,求![]() 的取值范圍.
的取值范圍.
(2)設函數(shù)![]() ,且
,且![]() ,求證:當
,求證:當![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
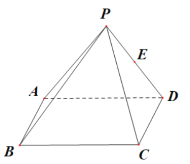
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() ,側面
,側面![]() 為等邊三角形且垂直于底面
為等邊三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中點.
的中點.
(1)在棱![]() 上取一點
上取一點![]() 使直線
使直線![]() ∥平面
∥平面![]() 并證明;
并證明;
(2)在(1)的條件下,當棱![]() 上存在一點
上存在一點![]() ,使得直線
,使得直線![]() 與底面
與底面![]() 所成角為
所成角為![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com