
【題目】如圖:已知四棱錐P—ABCD的底面ABCD是平行四邊形,PA⊥面ABCD,M是AD的中點,N是PC的中點.

(1)求證:MN∥面PAB;
(2)若平面PMC⊥面PAD,求證:CM⊥AD.
【答案】(1)詳見解析(2)詳見解析
【解析】
試題分析:(1)取BC中點E,連結ME、NE,由已知推導出平面PAB∥平面MNE,由此能證明MN∥平面PAB.
(2)利用面面垂直的性質,由平面PMC⊥平面PAD,平面ABCD⊥平面PAD,可證CM⊥平面PAD,由AD平面PAD,即可證明CM⊥AD
試題解析:(1)取PB的中點E,連接EA,EN,
在△PBC中,EN//BC且![]() ,
,
又![]() ,AD//BC,AD=BC
,AD//BC,AD=BC
所以EN//AM,,EN=AM.
所以四邊形ENMA是平行四邊形,
所以MN//AE. 又![]() ,
,![]() ,
,
所以MN//平面PAB.
(2)過點A作PM的垂線,垂足為H,
因為平面PMC⊥平面PAD,平面PMC∩平面PAD=PM,AH⊥PM,![]()
所以AH⊥平面PMC,又![]()
所以AH⊥CM.
因為PA⊥平面ABCD,![]() 所以PA⊥CM.
所以PA⊥CM.
因為PA∩AH=A,![]()
![]()
所以CM⊥平面PAD.
又![]() 所以CM⊥AD.
所以CM⊥AD.


科目:高中數學 來源: 題型:
【題目】如圖是正方體的平面展開圖,在這個正方體中,有以下四個命題:①![]() 平面ADNE;②
平面ADNE;②![]() 平面ABFE;③平面
平面ABFE;③平面![]() 平面AFN;④平面
平面AFN;④平面![]() 平面NCF.其中正確命題的序號是( )
平面NCF.其中正確命題的序號是( )
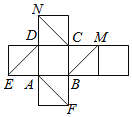
A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一種加熱食物的太陽灶,上面裝有可旋轉的拋物面形的反光鏡,鏡的軸截面是拋物線的一部分,盛食物的容器放在拋物線的焦點處,容器由若干根等長的鐵筋焊接在一起的架子支撐.已知鏡口圓的直徑為8m,鏡深1m.
(1)建立適當的坐標系,求拋物線的方程和焦點的位置;
(2)若把盛水和食物的容器近似地看作點,試求每根鐵筋的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列![]() 的前n項和為
的前n項和為![]() ,對于任意的
,對于任意的![]() ,都有
,都有![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求數列![]() 的通項公式;
的通項公式;
(3)令![]() 問是否存在正數m,使得
問是否存在正數m,使得![]() 對一切正整數n都成立?若存在,求出m的取值范圍;若不存在,請說明理由.
對一切正整數n都成立?若存在,求出m的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某中學舉行的物理知識競賽中,將三個年級參賽學生的成績在進行整理后分成5組,繪制出如圖所示的須率分布直方圖,圖中從左到右依次為第一、第二、第三、第四、第五小組.已知第三小組的頻數是15.

(1)求成績在50-70分的頻率是多少
(2)求這三個年級參賽學生的總人數是多少:
(3)求成績在80-100分的學生人數是多少
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 為平面向量,若存在不全為零的實數λ,μ使得λ
為平面向量,若存在不全為零的實數λ,μ使得λ![]() μ
μ![]() 0,則稱
0,則稱![]() 、
、![]() 線性相關,下面的命題中,
線性相關,下面的命題中,![]() 、
、![]() 、
、![]() 均為已知平面M上的向量.
均為已知平面M上的向量.
①若![]() 2
2![]() ,則
,則![]() 、
、![]() 線性相關;
線性相關;
②若![]() 、
、![]() 為非零向量,且
為非零向量,且![]() ⊥
⊥![]() ,則
,則![]() 、
、![]() 線性相關;
線性相關;
③若![]() 、
、![]() 線性相關,
線性相關,![]() 、
、![]() 線性相關,則
線性相關,則![]() 、
、![]() 線性相關;
線性相關;
④向量![]() 、
、![]() 線性相關的充要條件是
線性相關的充要條件是![]() 、
、![]() 共線.
共線.
上述命題中正確的是 (寫出所有正確命題的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點
的焦點![]() 為曲線
為曲線![]() 的一個焦點,
的一個焦點, ![]() 為坐標原點,點
為坐標原點,點![]() 為拋物線
為拋物線![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 軸的平行線交拋物線的準線于
軸的平行線交拋物線的準線于![]() ,直線
,直線![]() 交拋物線于點
交拋物線于點![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)若![]() 、
、![]() 、
、![]() 三個點滿足
三個點滿足![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站退出了關于生態文明建設進展情況的調查,調查數據表明,環境治理和保護問題仍是百姓最為關心的熱點,參與調查者中關注此問題的約占![]() .現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組
.現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
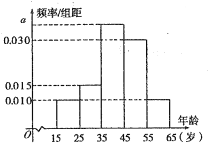
(1)求出![]() 的值;
的值;
(2)求這200人年齡的樣本平均數(同一組數據用該區間的中點值作代表)和中位數(精確到小數點后一位);
(3)現在要從年齡較小的第1,2組中用分層抽樣的方法抽取5人,再從這5人中隨機抽取3人進行問卷調查,求這2組恰好抽到2人的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com