【題目】已知等比數(shù)列
的前
項和為
，
且
為等差數(shù)列
的前三項．
（1）求
與數(shù)列
的通項公式；
（2）設(shè)數(shù)列
的前
項和
，試問是否存在正整數(shù)
，對任意的
使得
？若存在請求出
的最大值，若不存在請說明理由．
【答案】（1）
，
；（2）
的最大值為2．
【解析】
試題分析：（1）設(shè)等比數(shù)列
的公比為
，把
用
表示并列出等式，解得
，然后求得
，由等比數(shù)列前
項和公式寫出
，由此又可得出
的等差數(shù)列的前3項，從而得通項公式；（2）數(shù)列
，是等差數(shù)列相鄰項相乘的倒數(shù)，因此其前
項和用裂項相消法可求，從而得到
的取值范圍，不等式
成立，即
，因此只要
小于等于
最小值即可．
試題解析：（1）設(shè)等比數(shù)列的公比為，由
且
為等差數(shù)列
三項，
則
，得
，得
．
從而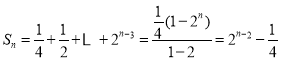
所以
的前三項為
，故等差數(shù)列的通項公式為．
（2）由（1）知，
所以數(shù)列
的前
項和
．
從而得對于
，
，故由知只要存在正整數(shù)
使
，
即只要
，解得
．
因為
為正整數(shù)，所以的最大值為2．
名校課堂系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】給出下列幾個命題：①三點確定一個平面；②一個點和一條直線確定一個平面；③垂直于同一直線的兩直線平行；④平行于同一直線的兩直線平行.其中正確命題的序號是____.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（1）用五點法畫出它在一個周期內(nèi)的閉區(qū)間上的圖象；
（2）指出
的周期和單調(diào)減區(qū)間
（3）說明此函數(shù)圖象可由
上的圖象經(jīng)怎樣的變換得到.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在一次數(shù)學(xué)測試中,有考生1 000名,現(xiàn)想了解這1 000名考生的數(shù)學(xué)成績,從中抽取100名學(xué)生的數(shù)學(xué)成績進行統(tǒng)計分析,在這個問題中,總體是指( )
A. 1 000名考生
B. 1 000名考生的數(shù)學(xué)成績
C. 100名考生的數(shù)學(xué)成績
D. 100名考生
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知若a=30.6，b=log3 0.6，c=0.63，則（ ）
A. a＞c＞b B. a＞b＞c C. c＞b＞a D. b＞c＞a
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某學(xué)校有男、女學(xué)生各500名.為了解男女學(xué)生在學(xué)習(xí)興趣與業(yè)余愛好方面是否存在顯著差異，擬從全體學(xué)生中抽取100名學(xué)生進行調(diào)查，則宜采用的抽樣方法是（ ）
A. 抽簽法 B. 隨機數(shù)法 C. 系統(tǒng)抽樣法 D. 分層抽樣法
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】從1，3，5，7中任取2個數(shù)字，從0，2，4，6，8中任取2個數(shù)字，組成沒有重復(fù)數(shù)字的四位數(shù)，其中能被5整除的四位數(shù)共有 個.（用數(shù)字作答）
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
