
【題目】已知函數![]() ,且
,且![]() .
.
(1)求函數![]() 的極值;
的極值;
(2)當![]() 時,證明:
時,證明:![]() .
.
【答案】(1)當![]() 時,函數
時,函數![]() 有極大值
有極大值![]() ,當
,當![]() 時,函數
時,函數![]() 有極小值
有極小值![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
試題分析:(1)求極值,可先求得導數![]() ,然后通過解不等式
,然后通過解不等式![]() 確定增區間,解不等式
確定增區間,解不等式![]() 確定減區間,則可得極大值和極小值;(2)要證明此不等式,我們首先研究不等式左邊的函數,記
確定減區間,則可得極大值和極小值;(2)要證明此不等式,我們首先研究不等式左邊的函數,記![]() ,求出其導數
,求出其導數![]() ,可知
,可知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,![]() ,這是
,這是![]() 時最小值,
時最小值,![]() ,這是
,這是![]() 時的最大值,因此要證明題中不等式,可分類,
時的最大值,因此要證明題中不等式,可分類,![]() 和
和![]() 分別證明.
分別證明.
試題解析:(1)依題意,![]() ,
,
故![]() ,
,
令![]() ,則
,則![]() 或
或![]() ; 令
; 令![]() ,則
,則![]() ,
,
故當![]() 時,函數
時,函數![]() 有極大值
有極大值![]() ,當
,當![]() 時,函數
時,函數![]() 有極小值
有極小值![]()
(2)由(1)知![]() ,令
,令![]() ,
,
則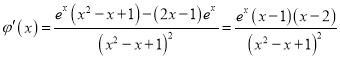 ,
,
可知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,令
上單調遞減,令![]() .
.
① 當![]() 時,
時,![]() ,所以函數
,所以函數![]() 的圖象在
的圖象在![]() 圖象的上方.
圖象的上方.
② 當![]() 時,函數
時,函數![]() 單調遞減,所以其最小值為
單調遞減,所以其最小值為![]() 最大值為2,而
最大值為2,而![]() ,所以函數
,所以函數![]() 的圖象也在
的圖象也在![]() 圖象的上方.
圖象的上方.
綜上可知,當![]() 時,
時,![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】下面程序執行后,輸出的值為( )
J=1;
A=0;
while J<5
J=J+1;
A=A+J* J;
end
print(%io(2),J);
A. 4 B. 5
C. 54 D. 55
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() 且
且![]() 為等差數列
為等差數列![]() 的前三項.
的前三項.
(1)求![]() 與數列
與數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 的前
的前![]() 項和
項和![]() ,試問是否存在正整數
,試問是否存在正整數![]() ,對任意的
,對任意的![]() 使得
使得![]() ?若存在請求出
?若存在請求出![]() 的最大值,若不存在請說明理由.
的最大值,若不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的奇函數f(x),設其導函數為f′(x),當x∈(-∞,0]時,恒有xf′(x)<f(-x),令F(x)=xf(x),則滿足F(3)>F(2x-1)的實數x的取值范圍是( )
A(![]() ,2) B(-2,1) C(-1,2) D(-1,
,2) B(-2,1) C(-1,2) D(-1,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】50.6,0.65,log0.55的大小順序是( )
A.0.65 < log0.65 < 50.6B.0.65 < 50.6< log0.65
C.log0.65 < 50.6 <0.65D.log0.65 <0.65 < 50.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,錯誤的是( )
A. 平行于同一條直線的兩個平面平行
B. 平行于同一個平面的兩個平面平行
C. 一個平面與兩個平行平面相交,交線平行
D. 一條直線與兩個平行平面中的一個相交,則必與另一個相交
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com