
【題目】已知函數![]() .
.
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)若關于![]() 的方程
的方程![]() 有四個不同的解
有四個不同的解![]() ,求實數
,求實數![]() 應滿足的條件;
應滿足的條件;
(3)在(2)條件下,若![]() 成等比數列,用
成等比數列,用![]() 表示t.
表示t.
【答案】(1)![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減;(2)
單調遞減;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)將![]() 代入,用分類討論的去掉絕對值符號后結合函數單調性性質得解;
代入,用分類討論的去掉絕對值符號后結合函數單調性性質得解;
(2)用分類討論的去掉絕對值符號得分段函數,然后用導數研究函數的單調性,求出滿足條件的![]() 的關系;
的關系;
(3)由韋達定理得![]() 兩兩互為倒數,結合等比數列性質及韋達定理可用
兩兩互為倒數,結合等比數列性質及韋達定理可用![]() 表示出
表示出![]() .
.
(1)![]() 時,
時, ,
,
易知在![]() 時,
時,![]() 是增函數,
是增函數,![]() 是減函數,
是減函數,
所以![]() 的單調增區間
的單調增區間![]() ,單調減區間是
,單調減區間是![]() .
.
(2) ,
,
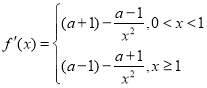 ,
,
當![]() 時,
時,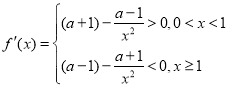
![]() 在
在![]() 是遞增,在
是遞增,在![]() 上遞減,不合題意;
上遞減,不合題意;
當![]() 時,
時, ![]() 時,由
時,由![]() 得
得![]() ,
,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 是單調遞增,
是單調遞增,
![]() 時,由
時,由![]() 得
得![]() ,
,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 是單調遞增,
是單調遞增,
又![]() ,
,![]() ,
,
∴實數![]() 應滿足的條件是
應滿足的條件是![]() .
.
(3)![]() ,即
,即![]() 或
或![]() ,
,
即![]() 或
或![]() ,
,
在![]() 中用
中用![]() 代換
代換![]() 得
得![]() ,即
,即![]() ,
,
∴方程![]() 與方程
與方程![]() 的根互為倒數.
的根互為倒數.
設這四個根從小到大依次為![]() ,則
,則![]() ,
,
所以![]() ,
,
若![]() 成等比數列,則
成等比數列,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:高中數學 來源: 題型:
【題目】王先生購買了一部手機,欲使用中國移動“神州行”卡或加入聯通的![]() 網,經調查其收費標準見下表:(注:本地電話費以分為計費單位,長途話費以秒為計費單位.)
網,經調查其收費標準見下表:(注:本地電話費以分為計費單位,長途話費以秒為計費單位.)
網絡 | 月租費 | 本地話費 | 長途話費 |
甲:聯通 |
|
|
|
乙:移動“神州行” | 無 |
|
|
若王先生每月撥打本地電話的時間是撥打長途電話時間的![]() 倍,若要用聯通
倍,若要用聯通![]() 應最少打多長時間的長途電話才合算.( )
應最少打多長時間的長途電話才合算.( )
A.![]() 秒B.
秒B.![]() 秒C.
秒C.![]() 秒D.
秒D.![]() 秒
秒
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高鐵、移動支付、網購與共享單車被稱為中國的新四大發明,為了解永安共享單車在淮南市的使用情況,永安公司調查了100輛共享單車每天使用時間的情況,得到了如圖所示的頻率分布直方圖.
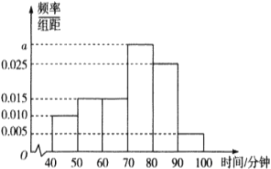
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)現在用分層抽樣的方法從前3組中隨機抽取8輛永安共享單車,將該樣本看成一個總體,從中隨機抽取2輛,求其中恰有1輛的使用時間不低于50分鐘的概率;
(Ⅲ)為進一步了解淮南市對永安共享單車的使用情況,永安公司隨機抽取了200人進行調查問卷分析,得到如下2×2列聯表:
經常使用 | 偶爾使用或不用 | 合計 | |
男性 | 50 | 100 | |
女性 | 40 | ||
合計 | 200 |
完成上述2×2列聯表,并根據表中的數據判斷是否有85%的把握認為淮南市使用永安共享單車的情況與性別有關?
附: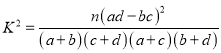
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線l過點
的直線l過點![]() ,以原點
,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的參數方程(
的參數方程(![]() 為常數)和曲線
為常數)和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求傾斜角
,求傾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人同時參加一次數學測試,共有![]() 道選擇題,每題均有
道選擇題,每題均有![]() 個選項,答對得
個選項,答對得![]() 分,答錯或不答得
分,答錯或不答得![]() 分.甲和乙都解答了所有的試題,經比較,他們只有
分.甲和乙都解答了所有的試題,經比較,他們只有![]() 道題的選項不同,如果甲最終的得分為
道題的選項不同,如果甲最終的得分為![]() 分,那么乙的所有可能的得分值組成的集合為____________.
分,那么乙的所有可能的得分值組成的集合為____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】地震波分為縱波和橫波,縱波傳播快,破壞性弱;橫波傳播慢,破壞性強.地震預警是指在地震發生后,利用地震波傳播速度小于電波傳播速度的特點,地震發生地提前對地震波尚未到達的地方進行預警.通過地震預警能在地震到達之前,為民眾爭取到更多逃生時間.2019年6月17日22時55分四川省宜賓市長寧縣發生6.0級地震,震源深度約16千米,震中長寧縣探測到縱波后4秒內通過電波向成都等地發出地震警報.已知縱波傳播速度約為5.5~7千米/秒,橫波傳播速度約為3.2~4千米/秒,長寧縣距成都約261千米,則成都預警時間(電波與橫波到達的時間差)可能為( )
A.51秒B.56秒C.61秒D.80秒
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為數列
為數列![]() 的前n項和, 且滿足
的前n項和, 且滿足![]() 為常數
為常數![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)是否存在實數 ![]() ,使得數列
,使得數列![]() 為等差數列?若存在,求出
為等差數列?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)當![]() 時,若數列
時,若數列![]() 滿足
滿足![]() ,且
,且![]() ,令
,令![]() ,求數列
,求數列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,且經過點
的中心在坐標原點,且經過點![]() ,它的一個焦點與拋物線
,它的一個焦點與拋物線![]() 的焦點重合.
的焦點重合.
(1)求橢圓![]() 的方程;
的方程;
(2)斜率為![]() 的直線過點
的直線過點![]() ,且與拋物線
,且與拋物線![]() 交于
交于![]() 兩點,設點
兩點,設點![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值;
的值;
(3)若直線![]() 過點
過點![]()
![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,直線
,直線![]() 的縱截距為
的縱截距為![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com