
請仔細閱讀以下材料:
已知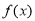 是定義在
是定義在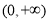 上的單調遞增函數.
上的單調遞增函數.
求證:命題“設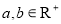 ,若
,若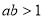 ,則
,則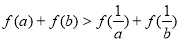 ”是真命題.
”是真命題.
證明:因為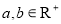 ,由
,由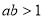 得
得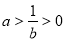 .
.
又因為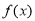 是定義在
是定義在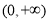 上的單調遞增函數,
上的單調遞增函數,
于是有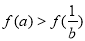 . ①
. ①
同理有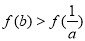 . ②
. ②
由① + ②得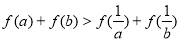 .
.
故,命題“設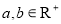 ,若
,若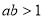 ,則
,則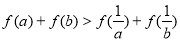 ”是真命題.
”是真命題.
請針對以上閱讀材料中的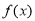 ,解答以下問題:
,解答以下問題:
(1)試用命題的等價性證明:“設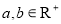 ,若
,若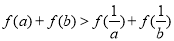 ,則:
,則: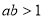 ”是真命題;
”是真命題;
(2)解關于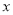 的不等式
的不等式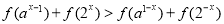 (其中
(其中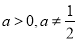 ).
).
(1)證明見解析;(2)①當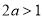 時,即
時,即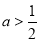 時,不等式的解集為:
時,不等式的解集為: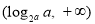
②當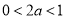 時,即
時,即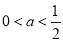 時,不等式的解集為:
時,不等式的解集為: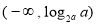
【解析】
試題分析:(1)在判斷四種命題的關系時,首先要分清命題的條件和結論,當確定了原命題時,要能根據四種命題的關系寫出其他三種命題;(2)當一個命題有大前提時,若要寫出其他三種命題,大前提需保持不變;(3)判斷一個命題為真命題,要給出推理證明;說明一個命題是假命題,只需舉出反例;(4)根據“原命題與逆否命題同真同假,逆命題與否命題同真同假”這一性質,當一個命題直接判斷不易進行時,可轉化為判斷其等價命題的真假.
試題解析: 【解析】
(1)原命題與原命題的逆否命題是等價命題.
原命題的逆否命題:設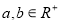 ,若
,若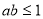 ,則:
,則: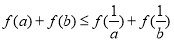 4分
4分
下面證明原命題的逆否命題為真命題:
因為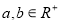 ,由
,由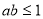 得:
得: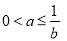 , 1分
, 1分
又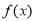 是定義在
是定義在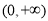 上的單調遞增函數
上的單調遞增函數
所以 (1) 1分
(1) 1分
同理有: (2) 1分
(2) 1分
由(1)+(2)得: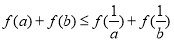 1分
1分
所以原命題的逆否命題為真命題
所以原命題為真命題. 1分
(2)由(1)的結論有: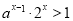 ,即:
,即: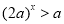 3分
3分
①當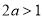 時,即
時,即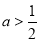 時,不等式的解集為:
時,不等式的解集為: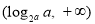 3分
3分
②當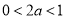 時,即
時,即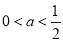 時,不等式的解集為:
時,不等式的解集為: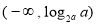 3分
3分
考點:1、命題及其相互關系;2、指數函數和對數函數的性質.


科目:高中數學 來源:2014-2015學年甘肅省高一上學期期末考試數學試卷(解析版) 題型:解答題
(本題滿分12分)已知直線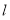 經過點
經過點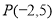 ,且斜率為
,且斜率為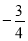 .
.
(Ⅰ)求直線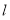 的方程;
的方程;
(Ⅱ)求與直線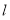 切于點(2,2),圓心在直線
切于點(2,2),圓心在直線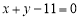 上的圓的方程.
上的圓的方程.
查看答案和解析>>
科目:高中數學 來源:[同步]2014年蘇教版必修三 3.4互斥事件練習卷(解析版) 題型:?????
如果事件A、B互斥,那么( )
A.A+B是必然事件 B.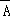 +
+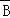 是必然事件 C.
是必然事件 C.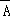 與
與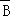 一定互斥 D.
一定互斥 D.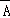 與
與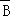 一定不互斥
一定不互斥
查看答案和解析>>
科目:高中數學 來源:[同步]2014年蘇教版必修三 3.4互斥事件練習卷(解析版) 題型:?????
同時擲兩枚硬幣,那么互為對立事件的是( )
A.至少有1枚正面和恰好有1枚正面
B.恰好有1枚正面和恰好有2枚正面
C.最多有1枚正面和至少有2枚正面
D.至少有2枚正面和恰好有1枚正面
查看答案和解析>>
科目:高中數學 來源:[同步]2014年蘇教版必修三 3.4互斥事件練習卷(解析版) 題型:?????
(2014•宜春模擬)第22屆冬季奧運會于2014年2月7日在俄羅斯索契開幕,到冰壺比賽場館服務的大學生志愿者中,有2名來自莫斯科國立大學,有4名來自圣彼得堡國立大學,現從這6名志愿者中隨機抽取2人,至少有1名志愿者來自莫斯科國立大學的概率是( )
A. B.
B.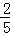 C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年重慶市高一上學期第三次定時練習數學試卷(解析版) 題型:解答題
(12分)(原創)已知函數 滿足以下條件:①定義在正實數集上;②
滿足以下條件:①定義在正實數集上;②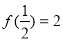 ;③對任意實數
;③對任意實數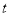 ,都有
,都有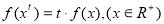 。
。
(1)求 ,
,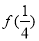 的值;
的值;
(2)求證:對于任意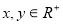 ,都有
,都有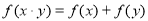 ;
;
(3)若不等式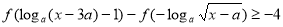 ,對
,對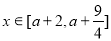 恒成立,求實數
恒成立,求實數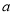 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com