
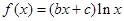 在
在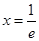 處取得極值,且在
處取得極值,且在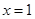 處的切線的斜率為1。
處的切線的斜率為1。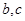 的值及
的值及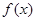 的單調(diào)減區(qū)間;
的單調(diào)減區(qū)間;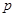 >0,
>0,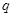 >0,
>0, ,求證:
,求證: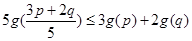 。
。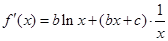
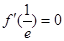 ,∴
,∴ 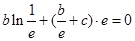 ,即
,即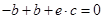 ,∴
,∴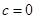
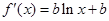 ,又
,又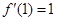 ,∴
,∴ 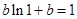 ,∴
,∴ 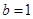
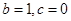
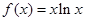 ,定義域為
,定義域為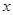 >0,
>0,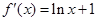
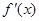 <0 得 0<
<0 得 0<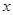 <
<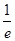 ,∴
,∴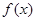 的單調(diào)減區(qū)間為
的單調(diào)減區(qū)間為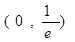 ……………6分
……………6分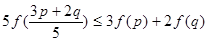
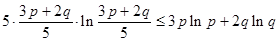
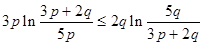
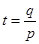 ,∵
,∵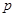 >0,
>0,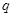 >0 ,∴
>0 ,∴ 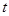 >0,即證
>0,即證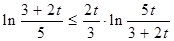
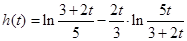 則
則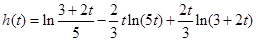
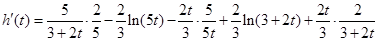
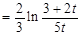
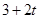 >
>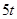 ,即0<
,即0<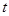 <1時,
<1時,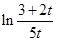 >0,即
>0,即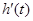 >0
>0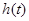 在(0,1)上遞增,∴
在(0,1)上遞增,∴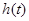 <
<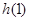 =0,
=0,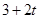 <
<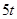 ,即
,即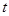 >1時,
>1時,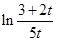 <0,即
<0,即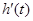 <0
<0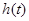 在(1,+∞)上遞減,∴
在(1,+∞)上遞減,∴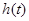 <
<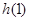 =0,
=0,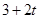 =
=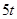 ,即
,即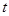 =1時,
=1時,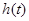 =
=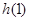 =0
=0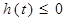 即
即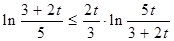
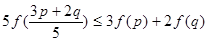
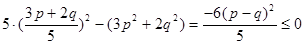
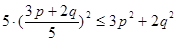
 ……………14分
……………14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
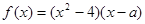
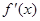 ;
;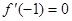 ,求
,求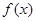 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
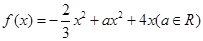
 在區(qū)間
在區(qū)間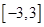 上的最小值和最大值;
上的最小值和最大值; 在區(qū)間
在區(qū)間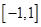 上是增函數(shù),求實數(shù)a的取值范圍。
上是增函數(shù),求實數(shù)a的取值范圍。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
 在定義域
在定義域 內(nèi)可導(dǎo),其圖象如圖所示,記
內(nèi)可導(dǎo),其圖象如圖所示,記 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為 ,則滿足
,則滿足 的實數(shù)
的實數(shù) 的范圍是 .
的范圍是 . 
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com