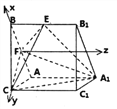
【題目】已知正三棱柱
中， 
分別為
的中點，設
.
（1）求證：平面
平面
；
（2）若二面角
的平面角為
，求實數
的值，并判斷此時二面角
是否為直二面角，請說明理由.
【答案】(1)見解析(2) 
二面角
為直二面角
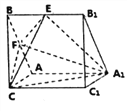
【解析】試題分析：（1）先證CF⊥平面A1EF，即可證明：平面A1CF⊥平面A1EF；
（2）如圖，以F為坐標原點， 
方向為
軸， 
軸正方向建立如圖所示空間直角坐標系，求出
，由定義則∠EFA1為二面角E﹣CF﹣A1的平面角，即可得出結論．
試題解析：
（1）因為正三棱柱
，所以
平面
，
所以
，
又
是正三角形， 
為
中點，
所以
，又
故
平面
，又
平面
，
所以平面
平面
.
（2）如圖，以
為坐標原點， 
方向為
軸， 
軸正方向建立如圖所示空間直角坐標系，不妨設底邊長
，由題意
，則
，
， 
， 
， 
，
， 
設平面
的法向量
則
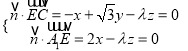，令
，
則
由（1）可知
為平面
的一個法向量
故
，計算可得： 
由（1）可知
， 
，
由定義則
為二面角
的平面角，
此時由勾股定理：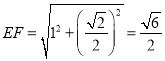 
， 
，
，
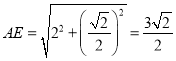滿足
，則
此時二面角
為直二面角
舉一反三期末百分沖刺卷系列答案科目：高中數學 來源： 題型：
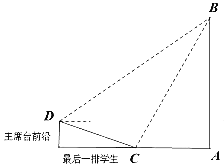
【題目】如圖,學校升旗儀式上，主持人站在主席臺前沿D處，測得旗桿AB頂部的仰角為
俯角最后一排學生C的俯角為
最后一排學生C測得旗桿頂部的仰角為
旗桿底部與學生在一個水平面上，并且不計學生身高.
(1)設
米,試用
和
表示旗桿的高度AB(米)；
(2)測得
米，
若國歌長度約為50秒，國旗班升旗手應以多大的速度勻速升旗才能是國旗到達旗桿頂點時師生的目光剛好停留在B處?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將正方形
沿對角線
折成直二面角
，有如下四個結論：
①
；
②
是等邊三角形；
③
與平面
所成的角為
；
④與
所成的角為.
其中錯誤的結論是____________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，從參加環保知識競賽的學生中抽出
名，將其成績（均為整數）整理后畫出的頻率分布直方圖如下：觀察圖形，回答下列問題：
（1）
這一組的頻數、頻率分別是多少？
（2）估計這次環保知識競賽成績的平均數、眾數、中位數。（不要求寫過程）
(3) 從成績是80分以上（包括80分）的學生中選兩人，求他們在同一分數段的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，且滿足
.
（1）判斷函數
在
上的單調性，并用定義證明；
（2）設函數
，求
在區間
上的最大值；
（3）若存在實數m，使得關于x的方程
恰有4個不同的正根，求實數m的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
為集合
的子集，且
，若
，則稱為集合的
元“大同集”.
（1）寫出實數集
的一個二元“大同集”；
（2）是否存在正整數集
的二元“大同集”，請說明理由；
（3）求出正整數集的所有三元“大同集”．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
