
【題目】已知函數![]() 的圖象過點P(1,2),且在
的圖象過點P(1,2),且在![]() 處取得極值
處取得極值
(1)求![]() 的值;
的值;
(2)求函數![]() 的單調區間;
的單調區間;
(3)求函數![]() 在
在![]() 上的最值.
上的最值.
【答案】(1)a="4," b=-3(2)單調增區間為![]() ,單調減區間為
,單調減區間為![]() (3)最大值為6,最小值為
(3)最大值為6,最小值為![]()
【解析】
試題(1)本題運用待定系數法求函數解析式,但函數圖象在x=![]() 處取得極值可得
處取得極值可得![]() ,通過解方程組可得到a、 b的值;(2)由導數性質求出f'(x)>0和f'(x)<0的x范圍就是函數f(x)的單調區間;(3)由函數在區間[-1,1]上的單調性:f(x)在
,通過解方程組可得到a、 b的值;(2)由導數性質求出f'(x)>0和f'(x)<0的x范圍就是函數f(x)的單調區間;(3)由函數在區間[-1,1]上的單調性:f(x)在![]() 上是減函數,在
上是減函數,在![]() 上是增函數求出函數的最值
上是增函數求出函數的最值
試題解析:(1) ∵函數f(x)=x3+ax2+bx(a,b![]() R)的圖象過點P(1,2)
R)的圖象過點P(1,2)
∴ f(1)=2 ∴ a+b=1
又函數f(x)在x=![]() 處取得極值點
處取得極值點
∴![]() (
(![]() )=0 因
)=0 因![]() (x)=3x2+2 ax+b ∴2a+3b="-1"
(x)=3x2+2 ax+b ∴2a+3b="-1"
解得 a="4," b="-3"
經檢驗 x=![]() 是f(x)極值點
是f(x)極值點
(2)由(1)得![]() (x)=3x2+8x-3令
(x)=3x2+8x-3令![]() (x) >0 ,得 x< -3或 x>
(x) >0 ,得 x< -3或 x>![]()
令![]() (x) <0 ,得 -3< x <
(x) <0 ,得 -3< x <![]()
函數f(x)的單調增區間為(![]() ,-3), (
,-3), (![]() ,
,![]() ),
),
函數f(x)的單調減區間為(-3,![]() )
)
(3) 由(2)知,又函數f(x)在x=![]() 處取得極小值點f(
處取得極小值點f(![]() )=
)=![]() f(-1)="6," f(1)="2"
f(-1)="6," f(1)="2"
函數f(x)在[-1,1]上的最大值為6,最小值為![]()


科目:高中數學 來源: 題型:
【題目】“石頭、剪刀、布”,又稱“猜丁殼”,是一種流行多年的猜拳游戲,起源于中國,然后傳到日本、朝鮮等地,隨著亞歐貿易的不斷發展,它傳到了歐洲,到了近代逐漸風靡世界.其游戲規則是:出拳之前雙方齊喊口令,然后在語音剛落時同時出拳,握緊的拳頭代表“石頭”,食指和中指伸出代表“剪刀”,五指伸開代表“布”.“石頭”勝“剪刀”、“剪刀”勝“布”、而“布”又勝過“石頭”.若所出的拳相同,則為和局.小軍和大明兩位同學進行“五局三勝制”的“石頭、剪刀、布”游戲比賽,則小軍和大明比賽至第四局小軍勝出的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
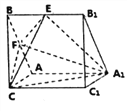
【題目】已知正三棱柱![]() 中,
中, ![]() 分別為
分別為![]() 的中點,設
的中點,設![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角為
的平面角為![]() ,求實數
,求實數![]() 的值,并判斷此時二面角
的值,并判斷此時二面角![]() 是否為直二面角,請說明理由.
是否為直二面角,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本題共3個小題,第1小題滿分3分,第2小題滿分6分,第3小題滿分9分.
已知數列![]() 滿足
滿足![]() .
.
(1)若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 是公比為
是公比為![]() 等比數列,
等比數列,![]() ,
,![]() 求
求![]() 的取值范圍;
的取值范圍;
(3)若![]() 成等差數列,且
成等差數列,且![]() ,求正整數
,求正整數![]() 的最大值,以及
的最大值,以及![]() 取最大值時相應數列
取最大值時相應數列![]() 的公差.
的公差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數![]() (實數
(實數![]() 、
、![]() 為常數),且滿足
為常數),且滿足![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)試判斷函數![]() 在區間
在區間![]() 上的單調性,并用函數單調性定義證明;
上的單調性,并用函數單調性定義證明;
(3)當![]() 時,函數
時,函數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】先后拋擲兩枚骰子,設出現的點數之和是12,11,10的概率依次是P1,P2,P3,則( )
(A)P1=P2<P3 (B)P1<P2<P3 (C)P1<P2=P3 (D)P3=P2<P1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com