近日，國家經貿委發出了關于深入開展增產節約運動，大力增產市場適銷對路產品的通知，并發布了當前國內市場185種適銷工業品和42種滯銷產品的參考目錄．為此，一公司舉行某產品的促銷活動，經測算該產品的銷售量P萬件（生產量與銷售量相等）與促銷費用x萬元滿足
(其中
，a為正常數)．已知生產該產品還需投入成本10+2P萬元(不含促銷費用)，產品的銷售價格定為
元／件．
(1)將該產品的利潤y萬元表示為促銷費用x萬元的函數；
(2)促銷費用投入多少萬元時，廠家的利潤最大．
（1）
，（
）.
（2）當
時,促銷費用投入1萬元時，廠家的利潤最大;
當
時,促銷費用投入
萬元時，廠家的利潤最大 .
解析試題分析：（1）由題意得到
， 將
代入化簡即得，（）.
（2）將原函數變形，應用基本不等式，
，
當且僅當
時，上式取等號.根據，討論，,的不同情況，確定最大利潤.
試題解析：（1）由題意知， ，
將代入化簡得：，（）， 6分
（2）
，
當且僅當時，上式取等號. 9分
當時,促銷費用投入1萬元時，廠家的利潤最大;
當時,
在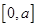
上單調遞增,所以在
時,函數有最大值．促銷費用投入萬元時，廠家的利潤最大 .
綜上述,當時,促銷費用投入1萬元時，廠家的利潤最大;
當時,促銷費用投入萬元時，廠家的利潤最大 . 12分
考點：函數的應用問題，基本不等式.
智能訓練練測考系列答案科目：高中數學 來源： 題型：解答題
已知函數
.
（1）若
的定義域和值域均是
，求實數
的值；
（2）若在區間
上是減函數，且對任意的
，都有
，求實數的取值范圍；
（3）若
，且對任意的
，都存在
，使得
成立，求實數的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知實數
，函數
.
（1）當
時，求
的最小值;
（2）當時,判斷的單調性,并說明理由；
（3）求實數
的范圍，使得對于區間
上的任意三個實數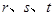
，都存在以
為邊長的三角形.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）某醫藥研究所開發的一種新藥,如果成年人按規定的劑量服用,據監測：服藥后每毫升血液中的含藥量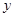
（單位：微克）與時間
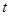（單位：小時）之間近似滿足如圖所示的曲線．
（Ⅰ）寫出第一次服藥后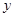與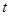之間的函數關系式
；
（Ⅱ）據進一步測定：每毫升血液中含藥量不少于
微克時，治療有效．問：服藥多少小時開始有治療效果？治療效果能持續多少小時？（精確到0．1）（參考數據：
）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
；
，x∈[3，5]；
(x>1)．
.
的不等式
；
在區間
上恒成立，求實數
的取值范圍.
，其中
為常數
為奇函數，試確定
恒成立，求實數
的定義域；
為何值時，函數值大于1.
.
時，指出
的單調遞減區間和奇偶性（不需說明理由）；
的零點；
不等式
恒成立，求實數
的取值范圍。