
設定點M(3, )與拋物線
)與拋物線 =2x上的點P的距離為
=2x上的點P的距離為 ,P到拋物線準線l的距為
,P到拋物線準線l的距為 ,則
,則 +
+ 取最小值時,P點的坐標為
取最小值時,P點的坐標為
| A.(0,0) | B.(1, ) ) | C.(2,2) | D.( ,- ,- ) ) |
C
解析試題分析:先判斷出M(3, )在拋物線
)在拋物線 =2x的外部然后做出圖形(如下圖)則PM=d1過p作PN⊥直線x=
=2x的外部然后做出圖形(如下圖)則PM=d1過p作PN⊥直線x= 則PN=d2,根據拋物線的定義可得d1+d2=PM+PF故要使
則PN=d2,根據拋物線的定義可得d1+d2=PM+PF故要使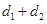 取最小值則只有當P,M,F三點共線時成立因此可求出MF所在的直線方程然后與拋物線的方程聯立即可求出P點的坐標.
取最小值則只有當P,M,F三點共線時成立因此可求出MF所在的直線方程然后與拋物線的方程聯立即可求出P點的坐標.
∵(3,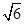 )在拋物線
)在拋物線 =2x上且
=2x上且 >
>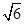 ∴M(3,
∴M(3, )在拋物線
)在拋物線 =2x的外部,∵拋物線y2=2x的焦點F(
=2x的外部,∵拋物線y2=2x的焦點F( ,0),準線方程為x=-
,0),準線方程為x=- ∴在拋物線
∴在拋物線 =2x上任取點P過p作PN⊥直線x=
=2x上任取點P過p作PN⊥直線x= 則PN=
則PN=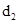
∴根據拋物線的定義可得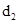 =PF,∴
=PF,∴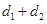 =PM+PF,∵PM+PF
=PM+PF,∵PM+PF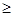 MF,∴當P,M,F三點共線時d1+d2取最小值,此時MF所在的直線方程為y-
MF,∴當P,M,F三點共線時d1+d2取最小值,此時MF所在的直線方程為y- =
= (x-3)即4x-3y-2=0,令4x-3y-2=0,
(x-3)即4x-3y-2=0,令4x-3y-2=0, =2x,聯立方程組得到 x-=2,y=2,即當點的坐標為(2,2)時,
=2x,聯立方程組得到 x-=2,y=2,即當點的坐標為(2,2)時,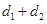 取最小值,故選C
取最小值,故選C
考點:拋物線的性質
點評:本題主要考察拋物線的性質,屬常考題,較難.解題的關鍵是將d1+d2=PM+PN根據拋物線的定義轉化為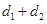 =PM+PF.
=PM+PF.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案科目:高中數學 來源: 題型:單選題
北京奧運會主體育場“鳥巢”的簡化鋼結構俯視圖如圖所示,內外兩圈的鋼骨架是離心率相同的橢圓,從外層橢圓頂點A、B向內層橢圓引切線AC、BD設內層橢圓方程為 +
+ =1(a
=1(a b
b 0),外層橢圓方程為
0),外層橢圓方程為 +
+ =1(a
=1(a b
b 0,m
0,m 1),AC與BD的斜率之積為-
1),AC與BD的斜率之積為- ,則橢圓的離心率為( )
,則橢圓的離心率為( )
A. B.
B. C.
C.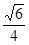 D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com