【題目】某城市為鼓勵人們綠色出行，乘坐地鐵，地鐵公司決定按照乘客經過地鐵站的數量實施分段優惠政策，不超過
站的地鐵票價如下表：
乘坐站數 |
|
|
|
票價（元） |
|
|
|
現有甲、乙兩位乘客同時從起點乘坐同一輛地鐵，已知他們乘坐地鐵都不超過
站，且他們各自在每個站下車的可能性是相同的.
（1）若甲、乙兩人共付費
元，則甲、乙下車方案共有多少種？
（2）若甲、乙兩人共付費
元，求甲比乙先到達目的地的概率.
【答案】(1)9(2) 
【解析】試題分析：（1）由題意知甲、乙乘坐地鐵均不超過
站，前
站設為
， 
， 
，（2），甲、乙兩人共有
種下車方案；（2）設
站分別為
， 
， 
， 
， 
， 
， 
， 
， 
，因為甲、乙兩人共付費
元，共有甲付
元，乙付
元；甲付
元，乙付
元；甲付
元，乙付
元三類情況. 由（1）可知每類情況中有
種方案，所以甲、乙兩人共付費
元共有
種方案. 而甲比乙先到達目的地的方案有共
種，從而得到甲比乙先到達目的地的概率.
試題解析：
（1）由題意知甲、乙乘坐地鐵均不超過
站，前
站設為
， 
， 
，
甲、乙兩人共有
， 
， 
， 
， 
， 
， 
， 
， 
種下車方案.
（2）設
站分別為
， 
， 
， 
， 
， 
， 
， 
， 
，因為甲、乙兩人共付費
元，共有甲付
元，乙付
元；甲付
元，乙付
元；甲付
元，乙付
元三類情況.
由（1）可知每類情況中有
種方案，所以甲、乙兩人共付費
元共有
種方案.
而甲比乙先到達目的地的方案有
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共
種，
故所求概率為
.
所以甲比乙先到達目的地的概率為
.
53隨堂測系列答案科目：高中數學 來源： 題型：
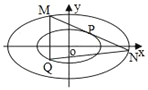
【題目】已知橢圓系方程
： 
(
， 
)， 
是橢圓
的焦點， 
是橢圓
上一點，且
.
（1）求
的離心率并求出
的方程；
（2）
為橢圓
上任意一點，過
且與橢圓
相切的直線
與橢圓
交于
， 
兩點，點
關于原點的對稱點為
，求證： 
的面積為定值，并求出這個定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】三棱錐
中，側面
底面
, 
是等腰直角三角形
的斜邊，且
.
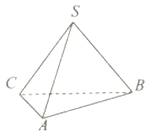
（1）求證： 
；
（2）已知平面
平面
，平面
平面
， 
，且
到平面
的距離相等，試確定直線
及點
的位置（說明作法及理由），并求三棱錐
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知橢圓
的離心率為
， 
， 
分別為橢圓的上頂點和右焦點， 
的面積為
，直線
與橢圓交于另一個點
，線段
的中點為
.
（1）求直線
的斜率；
（2）設平行于
的直線
與橢圓交于不同的兩點
， 
，且與直線
交于點
，求證：存在常數
，使得
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】11月11日有2000名網購者在某購物網站進行網購消費（金額不超過1000元），其中女性1100名，男性900名.該購物網站為優化營銷策略，根據性別采用分層抽樣的方法從這2000名網購者中抽取200名進行分析，如表.（消費金額單位：元）
（1）計算
的值，在抽出的200名且消費金額在
的網購者中隨機抽出2名發放網購紅包，求選出的2人均為女性的概率；
（2）若消費金額不低于600元的網購者為“網購達人”，低于600元的網購者為“非網購達人”，根據以上數據列
列聯表，并回答能否有
的把握認為“是否為網購達人與性別有關？”附：
，
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
