
分析 A、B、C三點共線,則$\overrightarrow{AB}$=λ$\overrightarrow{AC}$,化簡可得2a+b=1.根據 $\frac{1}{a}$+$\frac{2}{b}$=($\frac{1}{a}$+$\frac{2}{b}$)(2a+b),利用基本不等式求得它的最小值
解答 解:向量$\overrightarrow{OA}$=(1,-2),$\overrightarrow{OB}$=(a,-1),$\overrightarrow{OC}$=(-b,0),其中O為坐標原點,a>0,b>0,
∴$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=(a-1,1),$\overrightarrow{AC}$=$\overrightarrow{OC}$-$\overrightarrow{OA}$=(-b-1,2),
∵A、B、C三點共線,
∴$\overrightarrow{AB}$=λ$\overrightarrow{AC}$,
∴$\left\{\begin{array}{l}{a-1=λ(-b-1)}\\{1=2λ}\end{array}\right.$,
解得2a+b=1,
∴$\frac{1}{a}$+$\frac{2}{b}$=($\frac{1}{a}$+$\frac{2}{b}$)(2a+b)=2+2+$\frac{b}{a}$+$\frac{4a}{b}$≥4+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$=8,當且僅當a=$\frac{1}{4}$,b=$\frac{1}{2}$,取等號,
故$\frac{1}{a}$+$\frac{2}{b}$的最小值為8,
故答案為:8
點評 本題主要考查兩個向量共線的性質,兩個向量坐標形式的運算,基本不等式的應用,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | $\sqrt{5}$ | C. | $\sqrt{17}$ | D. | $\sqrt{17}$或$\frac{\sqrt{17}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
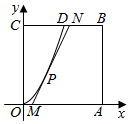 某地要建造一個邊長為2(單位:km)的正方形市民休閑公園OABC,將其中的區域ODC開挖成一個池塘,如圖建立平面直角坐標系后,點D的坐標為(1,2),曲線OD是函數y=ax2圖象的一部分,對邊OA上一點M在區域OABD內作一次函數y=kx+b(k>0)的圖象,與線段DB交于點N(點N不與點D重合),且線段MN與曲線OD有且只有一個公共點P,四邊形MABN為綠化風景區:
某地要建造一個邊長為2(單位:km)的正方形市民休閑公園OABC,將其中的區域ODC開挖成一個池塘,如圖建立平面直角坐標系后,點D的坐標為(1,2),曲線OD是函數y=ax2圖象的一部分,對邊OA上一點M在區域OABD內作一次函數y=kx+b(k>0)的圖象,與線段DB交于點N(點N不與點D重合),且線段MN與曲線OD有且只有一個公共點P,四邊形MABN為綠化風景區:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $m<\frac{5}{2}$ | B. | $m>\frac{5}{2}$ | C. | m<2 | D. | m>2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1,2,3,4} | B. | {-4,1,2,3} | C. | {1,2,3} | D. | {-1,4,2} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com