
【題目】已知函數![]()
(1)若函數![]() 在區間
在區間![]() 上單調遞減,求實數a的取值范圍;
上單調遞減,求實數a的取值范圍;
(2)當![]() ,(
,(![]() )時,求證:
)時,求證:![]() ;
;
(3)若函數![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,求證:
,求證:![]() (e為自然對數的底數)
(e為自然對數的底數)
【答案】(1)![]() ;(2)見解析;(3)見解析
;(2)見解析;(3)見解析
【解析】
(1)由題意可知![]() 在
在![]() 上恒成立,通過參變分離可知
上恒成立,通過參變分離可知![]() 恒成立,結合導數可求出
恒成立,結合導數可求出![]() 的最大值,從而可求出實數a的取值范圍.
的最大值,從而可求出實數a的取值范圍.
(2)由(1)可知![]() ,從而可知
,從而可知![]() ,結合累加法可知
,結合累加法可知![]() ,進而可證出
,進而可證出![]() .
.
(3)由題意可知![]() 有兩個相異實根
有兩個相異實根![]() ,
,![]() ,進而可知
,進而可知![]() ,結合導數證明
,結合導數證明![]() 在
在![]() 成立,從而可知
成立,從而可知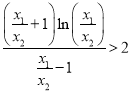 ,進而可知
,進而可知![]() .
.
解:(1)![]() ,若函數
,若函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
則![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 區間
區間![]() 上恒成立,所以
上恒成立,所以![]() .
.
令![]() ,則
,則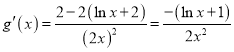 ,
,
因為![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,故
,故![]() ,所以實數a的取值范圍a
,所以實數a的取值范圍a![]() .
.
(2)由(1)可知,當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
所以,當![]() 時,
時,![]() ,則當
,則當![]() 時有
時有![]() ,
,
即![]() .因為當
.因為當![]() 時
時![]() ,所以
,所以![]() 時,
時,
![]() ,
,![]() ,
,
![]() ,……,
,……,![]() ,
,
所以![]()
![]() ,
,
即![]() ,所以
,所以![]() .
.
(3)若函數![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,不妨設
,不妨設![]() ,
,
即![]() 有兩個相異實根
有兩個相異實根![]() ,
,![]() ,且
,且![]() .
.
從而有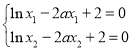 ,將上兩式相加得:
,將上兩式相加得:![]() .
.
將上兩式相減得:![]() ,從而
,從而![]() ,
,
即![]() ,即得
,即得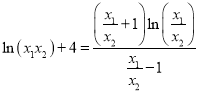 ,
,
要證明![]() ,也就是證明
,也就是證明![]() ,即
,即![]() ,
,
也就是證明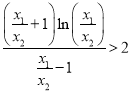 ,令
,令![]() ,只需證明
,只需證明![]() ,
,
由![]() ,知
,知![]() ,因此只需證明
,因此只需證明![]()
令![]() ,則
,則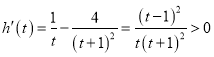 ,
,
所以![]() 在區間
在區間![]() 上單調遞增,又因為
上單調遞增,又因為![]() ,
,
因此![]() 在區間
在區間![]() 上恒成立.
上恒成立.
所以,當![]() 時,
時,![]() 成立,所以有
成立,所以有![]() 成立,從而
成立,從而![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).設
為參數).設![]() 與
與![]() 的交點為
的交點為![]() ,當
,當![]() 變化時,
變化時,![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)設![]() 為圓
為圓![]() 上任意一點,求
上任意一點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為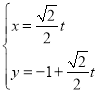 (t為參數),以原點O為極點,x正半軸為極軸建立極坐標系,曲線的極坐標方程為
(t為參數),以原點O為極點,x正半軸為極軸建立極坐標系,曲線的極坐標方程為![]() .
.
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)設P(0,-1),直線l與C的交點為M,N,線段MN的中點為Q,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
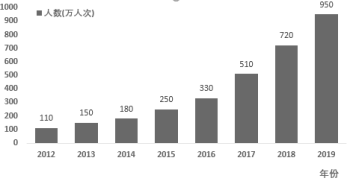
【題目】近年來,某市立足本地豐厚的文化旅游資源,以建設文化旅游強市,創建國家全域旅游示范市為引領,堅持以農為本,以鄉為魂,以旅促農,多元化推動產業化發展,文化和旅游扶貪工作卓有成效,精準扶貧穩步推進.該市旅游局為了更好的了解每年鄉村游人數的變化情況,繪制了如圖所示的柱狀圖.則下列說法錯誤的是( )
0
A.鄉村游人數逐年上升
B.相比于前一年,2015年鄉村游人數增長率大于2014年鄉村游人數增長率
C.近8年鄉村游人數的平均數小于2016年鄉村游人數
D.從2016年開始,鄉村游人數明顯增多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】向體積為1的正方體密閉容器內注入體積為![]() 的液體,旋轉容器,下列說法正確的是( )
的液體,旋轉容器,下列說法正確的是( )
A.當![]() 時,容器被液面分割而成的兩個幾何體完全相同
時,容器被液面分割而成的兩個幾何體完全相同
B.![]() ,液面都可以成正三角形形狀
,液面都可以成正三角形形狀
C.當液面與正方體的某條體對角線垂直時,液面面積的最大值為![]()
D.當液面恰好經過正方體的某條體對角線時,液面邊界周長的最小值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年以來,世界經濟和貿易增長放緩,中美經貿摩擦影響持續顯現,我國對外貿易仍然表現出很強的韌性.今年以來,商務部會同各省市全面貫徹落實穩外貿決策部署,出臺了一系列政策舉措,全力營造法治化、國際化、便利化的營商環境,不斷提高貿易便利化水平,外貿穩規模、提質量、轉動力取得階段性成效,進出口保持穩中提質的發展勢頭,下圖是某省近五年進出口情況統計圖,下列描述正確的是( )
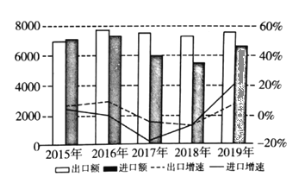
A.這五年,2015年出口額最少B.這五年,出口總額比進口總額多
C.這五年,出口增速前四年逐年下降D.這五年,2019年進口增速最快
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某蛋糕店制作并銷售一款蛋糕,制作一個蛋糕成本4元,且以9元的價格出售,若當天賣不完,剩下的則無償捐獻給飼料加工廠.根據以往100天的資料統計,得到如表需求量表:
需求量/個 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
天數 | 15 | 25 | 30 | 20 | 10 |
該蛋糕店一天制作了這款蛋糕X(X∈N)個,以x(單位:個,100≤x≤150,x∈N)表示當天的市場需求量,T(單位:元)表示當天出售這款蛋糕獲得的利潤.
(1)當x=135時,若X=130時獲得的利潤為T1,X=140時獲得的利潤為T2,試比較T1和T2的大小;
(2)當X=130時,根據上表,從利潤T不少于560元的天數中,按需求量分層抽樣抽取6天.
(i)求此時利潤T關于市場需求量x的函數解析式,并求這6天中利潤為650元的天數;
(ii)再從這6天中抽取3天做進一步分析,設這3天中利潤為650元的天數為ξ,求隨機變量ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是某市3月1日至14日的空氣質量指數趨勢圖,空氣質量指數小于100表示空氣質量優良,空氣質量指數大于200表示空氣重度污染,某人隨機選擇3月1日至3月13日中的某一天到達該市,并停留2天.
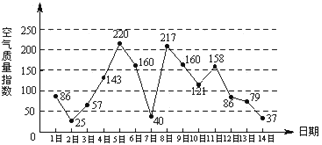
(Ⅰ)求此人到達當日空氣重度污染的概率;
(Ⅱ)設X是此人停留期間空氣質量優良的天數,求X的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com