【題目】已知函數
（1）求曲線
在點
處的切線方程；
（2）若函數
有兩個極值點
，
，且不等式
恒成立，求實數
的取值范圍.
通城學典默寫能手系列答案科目：高中數學 來源： 題型：
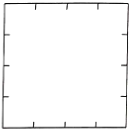
【題目】已知一塊邊長為4的正方形鋁板（如圖），請設計一種裁剪方法，用虛線標示在答題卡本題圖中，通過該方案裁剪，可焊接做成一個密封的正四棱柱（底面是正方形且側棱垂于底面的四棱柱），且該四棱柱的全面積等于正方形鋁板的面積（要求裁剪的塊數盡可能少，不計焊接縫的面積），則該四棱柱外接球的體積為________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】受疫情影響，某電器廠生產的空調滯銷，經研究決定，在已有線下門店銷售的基礎上，成立線上營銷團隊，大力發展“網紅”經濟，當線下銷售人數為
（人）時，每天線下銷售空調可達
（百臺），當線上銷售人數為
（人）（
）時，每天線上銷量達到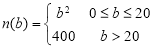
（百臺）.
（1）解不等式：
，并解釋其實際意義；
（2）若該工廠大有銷售人員
（
）人，按市場需求，安排人員進行線上或線下銷售，問該工廠每天銷售空調總臺數的最大值是多少百臺？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知曲線
的參數方程為：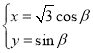
，（
為參數），以坐標原點為極點，
軸的非負半軸為極軸建立極坐標系，直線l的極坐標方程為
（1）求曲線和直線l的直角坐標方程；
（2）若點
在曲線上，且點到直線l的距離最小，求點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（1）若函數
在區間
上單調遞減，求實數a的取值范圍；
（2）當
，（
）時，求證：
；
（3）若函數有兩個極值點
，
，求證：
（e為自然對數的底數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正項數列
，
滿足：對任意正整數
，都有
，
，
成等差數列，，，
成等比數列，且
，
．
（Ⅰ）求證：數列
是等差數列；
（Ⅱ）求數列，的通項公式；
（Ⅲ）設
=
+
+…+
，如果對任意的正整數，不等式
恒成立，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中， 
，動點
滿足：以
為直徑的圓與
軸相切.
（1）求點
的軌跡方程；
（2）設點
的軌跡為曲線
，直線
過點
且與
交于
兩點，當
與
的面積之和取得最小值時，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
是平面
和平面
的交線，異面直線
，
分別在平面和平面內.
命題
：直線，中至多有一條與直線相交；
命題
：直線，中至少有一條與直線相交；
命題
：直線，都不與直線相交.
則下列命題中是真命題的為（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
