【題目】2020年春節前后，一場突如其來的新冠肺炎疫情在全國蔓延.疫情就是命令，防控就是責任.在黨中央的堅強領導和統一指揮下，全國人民眾志成城、團結一心，掀起了一場堅決打贏疫情防控阻擊戰的人民戰爭.下側的圖表展示了2月14日至29日全國新冠肺炎疫情變化情況，根據該折線圖，下列結論正確的是（ ）
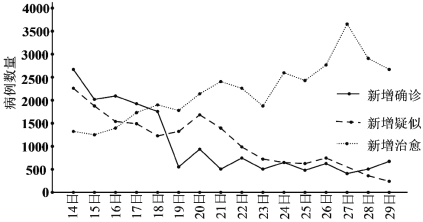
A.16天中每日新增確診病例數量呈下降趨勢且19日的降幅最大
B.16天中每日新增確診病例的中位數大于新增疑似病例的中位數
C.16天中新增確診、新增疑似、新增治愈病例的極差均大于
D.19日至29日每日新增治愈病例數量均大于新增確診與新增疑似病例之和
科目：高中數學 來源： 題型：
【題目】盲盒里面通常裝的是動漫、影視作品的周邊，或者設計師單獨設計出來的玩偶．由于盒子上沒有標注，購買者只有打開才會知道自己買到了什么，因此這種驚喜吸引了眾多年輕人，形成了“盲盒經濟”．某款盲盒內可能裝有某一套玩偶的
、
、
三種樣式，且每個盲盒只裝一個．
（1）若每個盲盒裝有、、三種樣式玩偶的概率相同．某同學已經有了樣式的玩偶，若他再購買兩個這款盲盒，恰好能收集齊這三種樣式的概率是多少？
（2）某銷售網點為調查該款盲盒的受歡迎程度，隨機發放了200份問卷，并全部收回．經統計，有
的人購買了該款盲盒，在這些購買者當中，女生占
；而在未購買者當中，男生女生各占
．請根據以上信息填寫下表，并分析是否有
的把握認為購買該款盲盒與性別有關？
女生 | 男生 | 總計 | |
購買 | |||
未購買 | |||
總計 |
參考公式：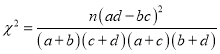
，其中
．
參考數據：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（3）該銷售網點已經售賣該款盲盒6周，并記錄了銷售情況，如下表：
周數 | 1 | 2 | 3 | 4 | 5 | 6 |
盒數 | 16 | ______ | 23 | 25 | 26 | 30 |
由于電腦故障，第二周數據現已丟失，該銷售網點負責人決定用第4、5、6周的數據求線性回歸方程，再用第1、3周數據進行檢驗．
①請用4、5、6周的數據求出
關于
的線性回歸方程
；
（注：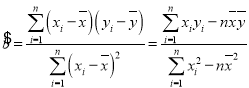
，
）
②若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2盒，則認為得到的線性回歸方程是可靠的，試問①中所得的線性回歸方程是否可靠？
③如果通過②的檢驗得到的回歸直線方程可靠，我們可以認為第2周賣出的盒數誤差也不超過2盒，請你求出第2周賣出的盒數的可能取值；如果不可靠，請你設計一個估計第2周賣出的盒數的方案．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某運動制衣品牌為了成衣尺寸更精準，現選擇15名志愿者，對其身高和臂展進行測量（單位：厘米），左圖為選取的15名志愿者身高與臂展的折線圖，右圖為身高與臂展所對應的散點圖，并求得其回歸方程為
，以下結論中不正確的為
A. 15名志愿者身高的極差小于臂展的極差
B. 15名志愿者身高和臂展成正相關關系，
C. 可估計身高為190厘米的人臂展大約為189.65厘米，
D. 身高相差10厘米的兩人臂展都相差11.6厘米，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左右焦點為
，
，離心率為
，過點且垂直于
軸的直線被橢圓
截得的弦長為1.
（1）求橢圓的方程；
（2）若直線
交橢圓于點
，
兩點，與線段
和橢圓短軸分別交于兩個不同點
，
，且
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
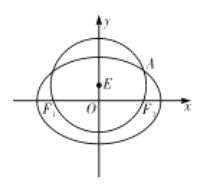
【題目】如圖，已知圓
經過橢圓
的左右焦點
，與橢圓
在第一象限的交點為
，且
， 
， 
三點共線.
（1）求橢圓
的方程；
（2）設與直線
（
為原點）平行的直線交橢圓
于
兩點，當
的面積取取最大值時，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知直線
的參數方程為
（
為參數），以坐標原點
為極點，
軸的非負半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）求直線的普通方程和曲線的直角坐標方程；
（2）設點
，直線與曲線的交點為
、
，求
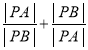的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
