【題目】已知函數(shù)
，且曲線
與直線
相切于點
，
（1）求
；
（2）若
，求實數(shù)
的取值范圍.
【答案】(1) 
；(2) 
【解析】
（1）先由題意得到
，求出
，再對函數(shù)求導，根據(jù)
求出
，從而可得到解析式；
（2）先令
，先由題意確定
，再由函數(shù)奇偶性的概念，易得到
為偶函數(shù)，因此只需
時，
；對函數(shù)求導，分別討論，
兩種情況，用導數(shù)的方法研究其單調(diào)性，最值等，即可得出結(jié)果.
（1）由題意可得：，解得
，
由
得
．
所以．
（2）令 ，
由得
，所以．
顯然為偶函數(shù)，所以只需時，．
，
當時，
，即在
上單調(diào)遞增，
所以
，
從而時，
成立．
當時，因為
在
上單調(diào)遞增，
又
時，
；
時，
，
所以存在
，使得
，
因此
時，
，
，即在
上單調(diào)遞減，
所以時，
，與矛盾，
因此時不成立．
綜上，滿足題設的
的取值范圍是
閱讀快車系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f(x)＝x3－3x及y＝f(x)上一點P(1，－2)，過點P作直線l.
(1)求使直線l和y＝f(x)相切且以P為切點的直線方程；
(2)求使直線l和y＝f(x)相切且切點異于點P的直線方程y＝g(x)．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某市春節(jié)期間7家超市的廣告費支出
（萬元）和銷售額
（萬元）數(shù)據(jù)如下：
超市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
參數(shù)數(shù)據(jù)及公式：
，
，
，
，
，
，
.
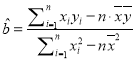（1）若用線性回歸模型擬合y與x的關系，求y關于x的線性回歸方程；
（2）用對數(shù)回歸模型擬合y與x的關系，可得回歸方程：
，經(jīng)計算得出線性回歸模型和對數(shù)模型的
分別約為0.75和0.97，請用說明選擇哪個回歸模型更合適，并用此模型預測A超市廣告費支出為8萬元時的銷售額.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在極坐標系中，曲線
的方程為
，以極點為原點，極軸所在直線為
軸建立直角坐標，直線
的參數(shù)方程為
（
為參數(shù)），與交于
，
兩點．
（1）寫出曲線的直角坐標方程和直線的普通方程；
（2）設點
；若
、
、
成等比數(shù)列，求
的值
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知直線
上有一動點
，過點作直線
垂直于
軸，動點
在上，且滿足
（
為坐標原點），記點的軌跡為曲線
.
（1）求曲線的方程；
（2）已知定點
，
，
為曲線上一點，直線
交曲線于另一點
，且點在線段
上，直線
交曲線于另一點
，求
的內(nèi)切圓半徑
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的右焦點為F，過點
的直線l與E交于A，B兩點.當l過點F時，直線l的斜率為
，當l的斜率不存在時，
.
（1）求橢圓E的方程.
（2）以AB為直徑的圓是否過定點？若過定點，求出定點的坐標；若不過定點，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為了了解一個小水庫中養(yǎng)殖的魚的有關情況，從這個水庫中多個不同位置捕撈出100條魚，稱得每條魚的質(zhì)量（單位：kg），并將所得數(shù)據(jù)分組，畫出頻率分布直方圖（如圖所示）．
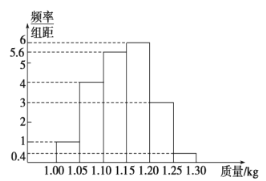
（1）在下面表格中填寫相應的頻率；
分組 | 頻率 |
| |
| |
| |
| |
| |
|
（2）估計數(shù)據(jù)落在
中的概率；
（3）將上面捕撈的100條魚分別作一記分組頻率號后再放回水庫．幾天后再從水庫的多處不同位置捕撈出120條魚，其中帶有記號的魚有6條．請根據(jù)這一情況來估計該水庫中魚的總條數(shù)．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下圖是一塊平行四邊形園地
，經(jīng)測量，
.擬過線段
上一點
設計一條直路
（點
在四邊形的邊上，不計直路的寬度），將該園地分為面積之比為
的左，右兩部分分別種植不同花卉.設
（單位：m）.
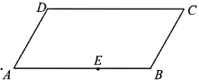
（1）當點與點
重合時，試確定點的位置；
（2）求
關于
的函數(shù)關系式；
（3）試確定點
的位置，使直路的長度最短.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
.
(1)若當
時，
取得極值，求
的值，并求的單調(diào)區(qū)間.
(2)若存在兩個極值點
，求的取值范圍，并證明：
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
