設a>0,函數f(x)=x2+a|lnx-1|.
(1)當a=1時,求曲線y=f(x)在x=1處的切線方程;
(2)當x∈[1,+∞)時,求函數f(x)的最小值.
【答案】
分析:(1)將a=1代入,對函數f(x)進行求導得到切線的斜率=f'(1),切點為(1,2),從而得到切線方程.
(2)分x≥e和x<e兩種情況討論.分別對函數f(x)進行求導,根據導函數的正負判斷出函數f(x)的單調性后可得到答案.
解答:解(1)當a=1時,f(x)=x
2+|lnx-1|
令x=1得f(1)=2,f'(1)=1,所以切點為(1,2),切線的斜率為1,
所以曲線y=f(x)在x=1處的切線方程為:x-y+1=0.
(2)①當x≥e時,f(x)=x
2+alnx-a,
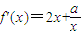
(x≥e)
∵a>0,
∴f(x)>0恒成立.
∴f(x)在[e,+∞)上增函數.
故當x=e時,y
min=f(e)=e
2②當1≤x<e時,f(x)=x
2-alnx+1,
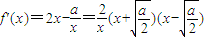
(1≤x<e)
(i)當
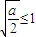
,即0<a≤2時,f'(x)在x∈(1,e)時為正數,
所以f(x)在區間[1,e)上為增函數.
故當x=1時,y
min=1+a,且此時f(1)<f(e)
(ii)當
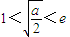
,即2<a<2e
2時,
f'(x)在
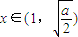
時為負數,在間
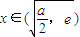
時為正數
所以f(x)在區間
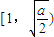
上為減函數,在
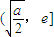
上為增函數
故當
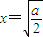
時,
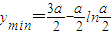
,
且此時
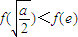
(iii)當
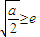
;即a≥2e
2時,
f'(x)在x∈(1,e)時為負數,
所以f(x)在區間[1,e]上為減函數,
當x=e時,y
min=f(e)=e
2.
綜上所述,當a≥2e
2時,f(x)在x≥e時和1≤x≤e時的最小值都是e
2.
所以此時f(x)的最小值為f(e)=e
2;
當2<a<2e
2時,f(x)在x≥e時的最小值為

,
而
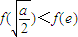
,
所以此時f(x)的最小值為
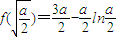
.
當0<a≤2時,在x≥e時最小值為e
2,在1≤x<e時的最小值為f(1)=1+a,
而f(1)<f(e),所以此時f(x)的最小值為f(1)=1+a
所以函數y=f(x)的最小值為
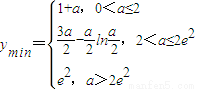 點評:
點評:本題主要考查函數導數的幾何意義和函數的單調性與其導函數的正負之間的關系.當導函數大于0時原函數單調遞增,當導函數小于0時原函數單調遞減.

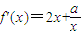 (x≥e)
(x≥e)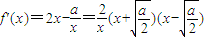 (1≤x<e)
(1≤x<e)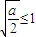 ,即0<a≤2時,f'(x)在x∈(1,e)時為正數,
,即0<a≤2時,f'(x)在x∈(1,e)時為正數,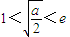 ,即2<a<2e2時,
,即2<a<2e2時,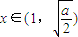 時為負數,在間
時為負數,在間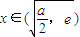 時為正數
時為正數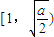 上為減函數,在
上為減函數,在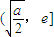 上為增函數
上為增函數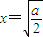 時,
時,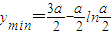 ,
,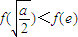
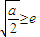 ;即a≥2e2時,
;即a≥2e2時, ,
,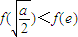 ,
,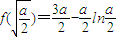 .
.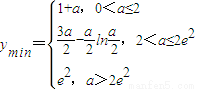


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案