
【題目】已知橢圓C: ![]() ,點P(4,0),過右焦點F作與y軸不垂直的直線l交橢圓C于A,B兩點. (Ⅰ)求橢圓C的離心率;
,點P(4,0),過右焦點F作與y軸不垂直的直線l交橢圓C于A,B兩點. (Ⅰ)求橢圓C的離心率;
(Ⅱ)求證:以坐標原點O為圓心與PA相切的圓,必與直線PB相切.
【答案】解:(Ⅰ)由題意可知:橢圓的焦點在x軸上,a=2,b= ![]() ,c=1,
,c=1,
則橢圓的離心率公式e= ![]() =
= ![]() ,
,
∴橢圓C的離心率 ![]() ;
;
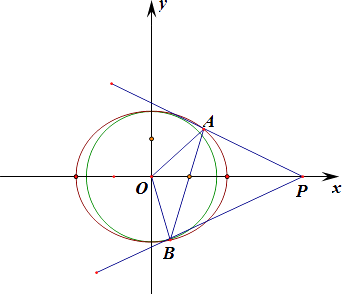
(Ⅱ)證明:由c=1,則焦點F(1,0),當直線l的斜率不存在時,直線l的方程x=1,
A,B兩點關于x軸對稱,則P(4,0)在x軸上,
∴直線PA與直線PB關于x軸對稱,
∴點O到直線PA的距離與到PB的距離相等,
∴以坐標原點O為圓心與PA相切的圓,必與直線PB相切,
當直線l的斜率存在時,設直線l:y=k(x﹣1),A(x1,y1),B(x2,y2),
由 ![]() ,整理得:(3+4k2)x2﹣8k2x+4k2﹣12=0,
,整理得:(3+4k2)x2﹣8k2x+4k2﹣12=0,
由韋達定理可知:x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
由kPA= ![]() =
= ![]() ,kPB=
,kPB= ![]() =
= ![]() ,
,
則kPA+kPB= ![]() +
+ ![]() =
= ![]() =
= 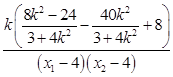 =0,
=0,
∴∠APO=∠BPO,則點O到直線PA和直線PB的距離相等,
∴以坐標原點O為圓心與PA相切的圓,必與直線PB相切.
【解析】(Ⅰ)由橢圓方程,求得a和c的值,即可求得橢圓的離心率;(2)分類討論,當直線斜率存在時,設直線方程,利用韋達定理及直線的斜率公式可知kPA+kPB=0,即可證明以坐標原點O為圓心與PA相切的圓,必與直線PB相切.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線C的頂點是原點,以x軸為對稱軸,且經過點P(1,2). (Ⅰ)求拋物線C的方程;
(Ⅱ)設點A,B在拋物線C上,直線PA,PB分別與y軸交于點M,N,|PM|=|PN|.求直線AB的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的奇函數,當x<0時,f(x)=ex(x+1),給出下列命題:
①當x>0時,f(x)=﹣e﹣x(x﹣1);
②函數f(x)有2個零點;
③f(x)<0的解集為(﹣∞,﹣1)∪(0,1),
④x1 , x2∈R,都有|f(x1)﹣f(x2)|<2.其中正確命題的個數是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應教育部頒布的《關于推進中小學生研學旅行的意見》,某校計劃開設八門研學旅行課程,并對全校學生的選擇意向進行調查(調查要求全員參與,每個學生必須從八門課程中選出唯一一門課程).本次調查結果整理成條形圖如下.圖中,已知課程A,B,C,D,E為人文類課程,課程F,G,H為自然科學類課程.為進一步研究學生選課意向,結合圖表,采取分層抽樣方法從全校抽取1%的學生作為研究樣本組(以下簡稱“組M”). 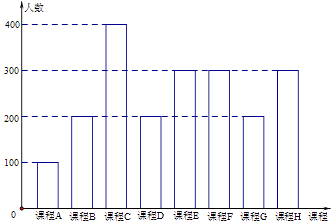
(Ⅰ)在“組M”中,選擇人文類課程和自然科學類課程的人數各有多少?
(Ⅱ)為參加某地舉辦的自然科學營活動,從“組M”所有選擇自然科學類課程的同學中隨機抽取4名同學前往,其中選擇課程F或課程H的同學參加本次活動,費用為每人1500元,選擇課程G的同學參加,費用為每人2000元.
(ⅰ)設隨機變量X表示選出的4名同學中選擇課程G的人數,求隨機變量X的分布列;
(ⅱ)設隨機變量Y表示選出的4名同學參加科學營的費用總和,求隨機變量Y的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中.點M不與點O重合,稱射線OM與圓x2+y2=1的交點N為點M的“中心投影點“. ⑴點M(1, ![]() )的“中心投影點”為
)的“中心投影點”為
⑵曲線x2 ![]() 上所有點的“中心投影點”構成的曲線的長度是 .
上所有點的“中心投影點”構成的曲線的長度是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在邊長為2的菱形ABCD中,∠BAD=60°,將△BCD沿對角線BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中點,FA⊥平面ABD,且FA=2 ![]() ,如圖2.
,如圖2. 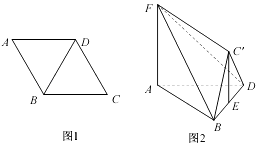
(1)求證:FA∥平面BC'D;
(2)求平面ABD與平面FBC'所成角的余弦值;
(3)在線段AD上是否存在一點M,使得C'M⊥平面FBC?若存在,求 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直三棱柱A1B1C1﹣ABC中, ![]() ,AB=AC=AA1=1,已知G和E分別為A1B1和CC1的中點,D與F分別為線段AC和AB上的動點(不包括端點),若GD⊥EF,則線段DF的長度的取值范圍為( )
,AB=AC=AA1=1,已知G和E分別為A1B1和CC1的中點,D與F分別為線段AC和AB上的動點(不包括端點),若GD⊥EF,則線段DF的長度的取值范圍為( )
A.[ ![]() ,1)
,1)
B.[ ![]() ,1]
,1]
C.( ![]() ,1)
,1)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() (m,n∈R)在x=1處取得極值2.
(m,n∈R)在x=1處取得極值2.
(1)求f(x)的解析式;
(2)k為何值時,方程f(x)-k=0只有1個根
(3)設函數g(x)=x2-2ax+a,若對于任意x1∈R,總存在x2∈[-1,0],使得g(x2)≤f(x1),求a的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com