
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 判斷f(x)的單調性,做出f(x)的草圖,得出f(x)=t的根的情況,根據方程t2-t+a=0不可能有兩個負根得出結論.
解答 解:當x<0時,f′(x)=-$\frac{1}{{x}^{2}}$-1<0,
∴f(x)在(-∞,0)上是減函數,
當x>0時,f(x)=|lnx|=$\left\{\begin{array}{l}{-lnx,0<x<1}\\{lnx,x≥1}\end{array}\right.$,
∴f(x)在(0,1)上是減函數,在[1,+∞)上是增函數,
做出f(x)的大致函數圖象如圖所示: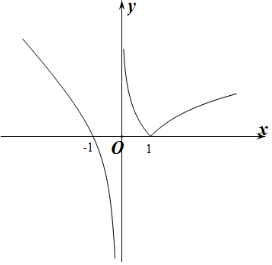
設f(x)=t,則當t<0時,方程f(x)=t有一解,
當t=0時,方程f(x)=t有兩解,
當t>0時,方程f(x)=t有三解.
由[f(x)]2-f(x)+a=0,得t2-t+a=0,
若方程t2-t+a=0有兩解t1,t2,則t1+t2=1,
∴方程t2-t+a=0不可能有兩個負實數根,
∴方程[f(x)]2-f(x)+a=0不可能有2個解.
故選A.
點評 本題考查了函數單調性的判斷,根的存在性判斷,一元二次方程的根的個數判斷,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
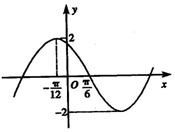 已知函數f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分圖象如圖所示,若將函數f(x)的圖象向右平移$\frac{π}{6}$個單位得到函數g(x)的圖象,則函數g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).
已知函數f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分圖象如圖所示,若將函數f(x)的圖象向右平移$\frac{π}{6}$個單位得到函數g(x)的圖象,則函數g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
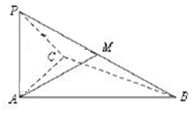 如圖,已知三棱錐P-ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M為PB的中點.
如圖,已知三棱錐P-ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M為PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com