
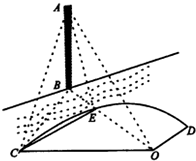
 如圖,河的一側是以O為圓形,半徑為80$\sqrt{3}$米的扇形區域OCD,河的另一側有一建筑物AB垂直于水平面,假設扇形OCD與點B處于同一水平面,記OB與$\widehat{CD}$的交點為E,若在點C,點O和點E處看到點A的仰角分別為45°,30°和60°,則∠CBO的余弦值為$\frac{4\sqrt{3}}{9}$.
如圖,河的一側是以O為圓形,半徑為80$\sqrt{3}$米的扇形區域OCD,河的另一側有一建筑物AB垂直于水平面,假設扇形OCD與點B處于同一水平面,記OB與$\widehat{CD}$的交點為E,若在點C,點O和點E處看到點A的仰角分別為45°,30°和60°,則∠CBO的余弦值為$\frac{4\sqrt{3}}{9}$. 分析 由題意,分別求出△CBO的三邊,利用余弦定理求角度.
解答 解:由題意,∠ABE=60°,∠ACB=45°,∠AOB=30°,所以∠EAB=30°,
所以AE=OE=80$\sqrt{3}$,并且建筑物AB垂直于水平面,
所以BE=40$\sqrt{3}$,所以OB=120$\sqrt{3}$,BC=AB=AE×$\frac{\sqrt{3}}{2}$=120,
在△CBO中,cos∠CBO=$\frac{B{C}^{2}+O{B}^{2}-O{C}^{2}}{2BC×OB}$=$\frac{12{0}^{2}+(120\sqrt{3})^{2}-(80\sqrt{3})^{2}}{2×120×120\sqrt{3}}$=$\frac{4\sqrt{3}}{9}$;
故答案為:$\frac{4\sqrt{3}}{9}$.
點評 本題考查了解三角形的實際應用;關鍵是將問題抽象出數學模型,利用余弦定理解三角形.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
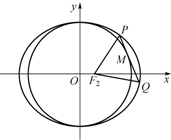 已知橢圓的長軸長為6,離心率為$\frac{1}{3}$,F2為橢圓的右焦點.
已知橢圓的長軸長為6,離心率為$\frac{1}{3}$,F2為橢圓的右焦點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com