
| A. | {x|x<-2或x>4} | B. | {x|x<-2或x>2} | C. | {x|x<0或x>4} | D. | {x|x<0或x>6} |
分析 由偶函數f(x)滿足f(x)=2-x-4(x≤0),可得f(x)=f(|x|)=2|x|-4,根據偶函數的性質將函數轉化為絕對值函數,然后求解不等式可得答案.
解答 解:由偶函數f(x)滿足f(x)=2-x-4(x≤0),故f(x)=f(|x|)=2|x|-4,
則f(x-2)=f(|x-2|)=2|x-2|-4,要使f(|x-2|)>0,
只需2|x-2|-4>0,|x-2|>2,解得x>4,或x<0.
故解集為:{x|x<0,或x>4}.
故選:C.
點評 本題主要考查偶函數性質、不等式的解法以及相應的運算能力,解答本題的關鍵是利用偶函數的性質將函數轉化為絕對值函數,屬基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | f(x)=$\frac{{2}^{x}+1}{x}$ | B. | f(x)=$\frac{ln({x}^{2}+2)}{x}$ | C. | f(x)=$\frac{{x}^{3}+3}{x}$ | D. | f(x)=$\frac{lnx}{x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)與f(x2)的大小不能確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦點分別為F1,F2,拋物線y2=4x與橢圓C有相同的焦點,且橢圓C過點$({1,\frac{3}{2}})$.
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦點分別為F1,F2,拋物線y2=4x與橢圓C有相同的焦點,且橢圓C過點$({1,\frac{3}{2}})$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
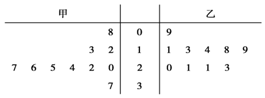 某籃球隊甲、乙兩名運動員練習罰球,每人練習10組,每組罰球40個.命中個數的莖葉圖如圖,則下面結論中錯誤的一個是( )
某籃球隊甲、乙兩名運動員練習罰球,每人練習10組,每組罰球40個.命中個數的莖葉圖如圖,則下面結論中錯誤的一個是( )| A. | 乙的眾數是21 | B. | 甲的中位數是24 | ||
| C. | 甲的極差是29 | D. | 甲罰球命中率比乙高 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 商店名稱 | A | B | C | D | E |
| 銷售額x(千萬元) | 3 | 5 | 6 | 7 | 9 |
| 利潤額y(千萬元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{{2^n}+1}}{{{2^{n-1}}}}$ | B. | $\frac{{{2^n}-1}}{{{2^{n-1}}}}$ | C. | $\frac{{{2^n}+1}}{{{2^{n+1}}}}$ | D. | $\frac{{{2^n}-1}}{{{2^{n+1}}}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向右平移$\frac{π}{3}$個單位 | B. | 向左平移$\frac{π}{4}$個單位 | ||
| C. | 向左平移$\frac{π}{3}$個單位 | D. | 向右平移$\frac{π}{4}$個單位 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com