
【題目】已知函數![]() ,
,![]() .
.
(1)記![]() ,試判斷
,試判斷![]() 在區間
在區間![]() 內零點個數并說明理由;
內零點個數并說明理由;
(2)記(1)中的![]() 在
在![]() 內的零點為
內的零點為![]() ,
, ,若
,若![]() 在
在![]() 有兩個不等實根
有兩個不等實根![]()
![]() ,判斷
,判斷![]() 與
與![]() 的大小,并給出對應的證明.
的大小,并給出對應的證明.
【答案】(1)一個零點,理由見解析;(2)![]() ,證明見解析
,證明見解析
【解析】
(1)利用導數得到![]() 在區間
在區間![]() 上是增函數,
上是增函數,![]() ,
,![]() ,并且
,并且![]() 在
在![]() 上連續的,由零點定理即得解;(2)先求出當
上連續的,由零點定理即得解;(2)先求出當![]() 時,
時,![]() 是單調遞增函數;當
是單調遞增函數;當![]() 時,
時,![]() 是單調遞減函數,轉化成證明
是單調遞減函數,轉化成證明![]() ,即轉化成證明
,即轉化成證明![]() .
.
(1)由題意:![]() ,
,
那么![]() ,定義域為
,定義域為![]() ,
,![]() ,
,
由題設![]() ,故
,故![]() ,即
,即![]() 在區間
在區間![]() 上是增函數.
上是增函數.
那么![]() ,
,![]() ,并且
,并且![]() 在
在![]() 上連續的,
上連續的,
故根據零點存在定理,有![]() 在區間
在區間![]() 有且僅有唯一實根,即一個零點.
有且僅有唯一實根,即一個零點.
(2) ,
,
當![]() 時,
時,![]() 恒大于
恒大于![]() ,
,
所以當![]() 時,
時,![]() 是單調遞增函數;
是單調遞增函數;
當![]() 時,
時,![]() 恒小于
恒小于![]() ,
,![]() 是單調遞減函數.
是單調遞減函數.![]() 在
在![]() 有兩個不等實根
有兩個不等實根![]() ,
,
則![]() ,
,![]() ,顯然:當
,顯然:當![]() 時,
時,![]() .
.
要證明![]() ,即可證明
,即可證明![]() ,
,
而![]() 在
在![]() 時是單調遞減函數.故證
時是單調遞減函數.故證![]() .
.
又由![]() ,即可證:
,即可證:![]() .即
.即![]() ,(構造思想),
,(構造思想),
即![]() ,
,
令![]() ,由(1)可知:
,由(1)可知:![]() ,
,
那么:![]() ,
,
記![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;故
;故![]() ;
;
而![]() ;故
;故![]() ,而
,而![]() ,從而有:
,從而有:![]() ;
;
因此:![]() ,即
,即![]() 單增,從而
單增,從而![]() 時,
時,![]() ,
,
即![]() 成立.故得:
成立.故得:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】若方程![]() 所表示的曲線為C,給出下列四個命題:
所表示的曲線為C,給出下列四個命題:
①若C為橢圓,則1<t<4且t≠![]() ;
;
②若C為雙曲線,則t>4或t<1;
③曲線C不可能是圓;
④若C表示橢圓,且長軸在x軸上,則1<t<![]() .
.
其中正確的命題是________(把所有正確命題的序號都填在橫線上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() :
:![]() (
(![]() ,
,![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() :
:![]() .
.
(1)說明![]() 是哪一種曲線,并將
是哪一種曲線,并將![]() 的方程化為極坐標方程;
的方程化為極坐標方程;
(2)若直線![]() 的方程為
的方程為![]() ,設
,設![]() 與
與![]() 的交點為
的交點為![]() ,
,![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() ,
,![]() ,若
,若![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() :
:![]() (
(![]() 為參數,
為參數,![]() ),曲線
),曲線![]() :
:![]() (
(![]() 為參數),
為參數),![]() 與
與![]() 相切于點
相切于點![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求![]() 的極坐標方程及點
的極坐標方程及點![]() 的極坐標;
的極坐標;
(2)已知直線![]() :
:![]() 與圓
與圓![]() :
:![]() 交于
交于![]() ,
,![]() 兩點,記
兩點,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
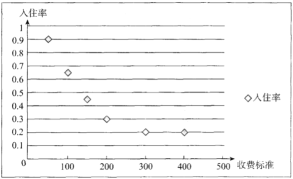
【題目】近年來,隨著互聯網技術的快速發展,共享經濟覆蓋的范圍迅速擴張,繼共享單車、共享汽車之后,共享房屋以“民宿”、“農家樂”等形式開始在很多平臺上線.某創業者計劃在某景區附近租賃一套農房發展成特色“農家樂”,為了確定未來發展方向,此創業者對該景區附近六家“農家樂”跟蹤調查了![]() 天.得到的統計數據如下表,
天.得到的統計數據如下表,![]() 為收費標準(單位:元/日),
為收費標準(單位:元/日),![]() 為入住天數(單位:),以頻率作為各自的“入住率”,收費標準
為入住天數(單位:),以頻率作為各自的“入住率”,收費標準![]() 與“入住率”
與“入住率”![]() 的散點圖如圖
的散點圖如圖
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
(1)若從以上六家“農家樂”中隨機抽取兩家深入調查,記![]() 為“入住率”超過
為“入住率”超過![]() 的農家樂的個數,求
的農家樂的個數,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散點圖判斷
,由散點圖判斷![]() 與
與![]() 哪個更合適于此模型(給出判斷即可,不必說明理由)?并根據你的判斷結果求回歸方程.(
哪個更合適于此模型(給出判斷即可,不必說明理由)?并根據你的判斷結果求回歸方程.(![]() 結果保留一位小數)
結果保留一位小數)
(3)若一年按![]() 天計算,試估計收費標準為多少時,年銷售額
天計算,試估計收費標準為多少時,年銷售額![]()
![]() 入住率
入住率![]() 收費標準
收費標準![]() )
)
參考數據: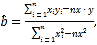
![]()
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
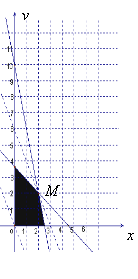
【題目】(本小題滿分13分)某縣一個化肥廠生產甲、乙兩種混合肥料,生產1車皮甲種肥料的主要原料是磷酸鹽4噸、硝酸鹽18噸;生產1車皮乙種肥料需要的主要原料是磷酸鹽1噸、硝酸鹽15噸.先庫存磷酸鹽10噸、硝酸鹽66噸,在此基礎上生產這兩種混合肥料.若生產1車皮甲種肥料產生的利潤為10000元;生產1車皮乙種肥料產生的利潤為5000元.那么分別生產甲、乙兩種肥料各多少車皮能產生最大的利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第16屆亞運會在中國廣州進行,為了搞好接待工作,組委會招幕了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,調查發現,男、女志愿者中分別有
名女志愿者,調查發現,男、女志愿者中分別有![]() 人和
人和![]() 人喜愛運動,其余人不喜愛運動.
人喜愛運動,其余人不喜愛運動.
(1)根據以上數據完成以下![]() 列聯表:
列聯表:
喜愛運動 | 不喜愛運動 | 總計 | |
男 |
|
| |
女 |
|
| |
總計 |
|
(2)根據列聯表的獨立性檢驗,能否在犯錯誤的概率不超過![]() 的前提下認為性別與喜愛運動有關?
的前提下認為性別與喜愛運動有關?
附:
|
|
|
|
|
|
|
|
|
|
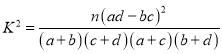 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com