【題目】（本小題滿分13分）某縣一個化肥廠生產甲、乙兩種混合肥料，生產1車皮甲種肥料的主要原料是磷酸鹽4噸、硝酸鹽18噸；生產1車皮乙種肥料需要的主要原料是磷酸鹽1噸、硝酸鹽15噸．先庫存磷酸鹽10噸、硝酸鹽66噸，在此基礎上生產這兩種混合肥料．若生產1車皮甲種肥料產生的利潤為10000元；生產1車皮乙種肥料產生的利潤為5000元．那么分別生產甲、乙兩種肥料各多少車皮能產生最大的利潤？
中考利劍中考試卷匯編系列答案
教育世家狀元卷系列答案
黃岡課堂作業本系列答案科目：高中數學 來源： 題型：
【題目】已知
是異面直線，
是空間一定點，下列命題中正確的個數為（ ）
①過點總可以作一條直線與都垂直；
②過點總可以作一個平面與都平行；
③過點總可以作一條直線與之一垂直于與另一條平行；
④過點總可以作一個平面與 之一垂直于與另一條平行；
⑤過點總可以作一個平面與直線同時垂直
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲袋中裝有2個白球，3個黑球，乙袋中裝有1個白球，2個黑球，這些球除顏色外完全相同.
（1）從兩袋中各取1個球，記事件
：取出的2個球均為白球，求
；
（2）每次從甲、乙兩袋中各取2個球，若取出的白球不少于2個就獲獎（每次取完后將球放回原袋），共取了3次，記獲獎次數為
，寫出的分布列并求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
.
（1）記
，試判斷
在區間
內零點個數并說明理由；
（2）記（1）中的在內的零點為
，
，若
在
有兩個不等實根
，判斷
與
的大小，并給出對應的證明.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
的離心率為
，且焦點到漸近線的距離為
．
（1）求雙曲線
的標準方程；
（2）若以
為斜率的直線
與雙曲線相交于兩個不同的點
，
，且線段
的垂直平分線與兩坐標軸圍成的三角形的面積為
，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】三角形面積為S=
(a+b+c)r,a,b,c為三角形三邊長,r為三角形內切圓半徑,利用類比推理,可以得出四面體的體積為 ( )
A. V=
abc B. V=Sh
C. V=(ab+bc+ac)·h(h為四面體的高) D. V=(S1+S2+S3+S4)·r(其中S1,S2,S3,S4分別為四面體四個面的面積,r為四面體內切球的半徑,設四面體的內切球的球心為O,則球心O到四個面的距離都是r)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”.三國時期，吳國的數學家趙爽創制了一幅“勾股圓方圖”，用數形結合的方法給出了勾股定理的詳細證明.如圖所示的“勾股圓方圖”中，四個相同的直角三角形與中間的小正方形拼成一個大正方形，若直角三角形中較小的銳角
，現在向該正方形區域內隨機地投擲100枚飛鏢，則估計飛鏢落在區域1的枚數最有可能是（ ）
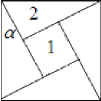
A.30B.40C.50D.60
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
