
【題目】某機構為了研究人的腳的大小與身高之間的關系,隨機測量了20人,得到如下數據:


(1) 若“身高大于175厘米”的為“高個”,“身高小于等于175厘米”的為“非高個”;“腳長大于42碼”的為“大腳”,“腳長小于等于42碼”的為“非大腳”,請根據上表數據完成下面的2×2列聯表.

(2)根據(1)中的2×2列聯表,在犯錯誤的概率不超過0.01的前提下,能否認為腳的大小與身高之間有關系?
![]() ,
,
![]()
科目:高中數學 來源: 題型:
【題目】一個直角三角形的三個頂點分別在底面棱長為2的正三棱柱的側棱上,則該直角三角形斜邊的最小值為__________.
【答案】![]()
【解析】 如圖,不妨設
如圖,不妨設![]() 在
在![]() 處,
處, ![]() ,
,
則有![]() 由
由![]()
![]() 該直角三角形斜邊
該直角三角形斜邊![]()
故答案為![]() .
.
【題型】填空題
【結束】
16
【題目】已知函數f(x)=![]() ,g(x)=
,g(x)=![]() ,若函數y=f(g(x))+a有三個不同的零點x1,x2,x3(其中x1<x2<x3),則2g(x1)+g(x2)+g(x3)的取值范圍為______.
,若函數y=f(g(x))+a有三個不同的零點x1,x2,x3(其中x1<x2<x3),則2g(x1)+g(x2)+g(x3)的取值范圍為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一次考試共有10道選擇題,每道選擇題都有4個選項,其中有且只有一個是正確的.評分標準規定:“每題只選一個選項,答對得5分,不答或答錯得零分”.某考生已確定有7道題的答案是正確的,其余題中:有一道題都可判斷兩個選項是錯誤的,有一道題可以判斷一個選項是錯誤的,還有一道題因不理解題意只好亂猜.試求出該考生:
(Ⅰ)得50分的概率;
(Ⅱ)所得分數![]() 的數學期望(用小數表示,精確到0.01k^s*5#u)
的數學期望(用小數表示,精確到0.01k^s*5#u)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 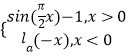 (a>0,且a≠1)的圖象上關于y軸對稱的點至少有5對,則實數a的取值范圍是( )
(a>0,且a≠1)的圖象上關于y軸對稱的點至少有5對,則實數a的取值范圍是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解高中生作文成績與課外閱讀量之間的關系,某研究機構隨機抽取了60名高中生,通過問卷調查,得到以下數據:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

由以上數據,計算得到K2的觀測值k≈9.643,根據臨界值表,以下說法正確的是( )
A. 沒有充足的理由認為課外閱讀量大與作文成績優秀有關
B. 有0.5%的把握認為課外閱讀量大與作文成績優秀有關
C. 有99.9%的把握認為課外閱讀量大與作文成績優秀有關
D. 有99.5%的把握認為課外閱讀量大與作文成績優秀有關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,已知圓C的圓心坐標為(2,0),半徑為 ![]() ,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系.,直線l的參數方程為:
,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系.,直線l的參數方程為: ![]() (t為參數).
(t為參數).
(1)求圓C和直線l的極坐標方程;
(2)點P的極坐標為(1, ![]() ),直線l與圓C相交于A,B,求|PA|+|PB|的值.
),直線l與圓C相交于A,B,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cos2ωx+2 ![]() sinωxcosωx﹣1,且f(x)的周期為2.
sinωxcosωx﹣1,且f(x)的周期為2.
(Ⅰ)當 ![]() 時,求f(x)的最值;
時,求f(x)的最值;
(Ⅱ)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,網格紙上小正方形的邊長為1,粗線畫出的是一正方體被截去一部分后所得幾何體的三視圖,則該幾何體的表面積為( ) 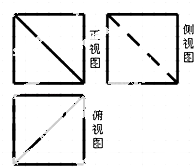
A.54
B.162
C.54+18 ![]()
D.162+18 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方向向量為v=(1, ![]() )的直線l過點(0,﹣2
)的直線l過點(0,﹣2 ![]() )和橢圓C:
)和橢圓C: ![]() =1(a>b>0)的焦點,且橢圓C的中心關于直線l的對稱點在橢圓C的右準線上.
=1(a>b>0)的焦點,且橢圓C的中心關于直線l的對稱點在橢圓C的右準線上.
(Ⅰ)求橢圓C的方程;
(Ⅱ)是否存在過點E(﹣2,0)的直線m交橢圓C于點M、N,滿足 ![]() =
= ![]() .cot∠MON≠0(O為原點).若存在,求直線m的方程;若不存在,請說明理由.
.cot∠MON≠0(O為原點).若存在,求直線m的方程;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com