
已知數列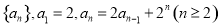
⑴求證: 為等差數列;
為等差數列;
⑵求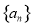 的前n項和
的前n項和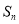 ;
;
⑶若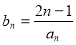 ,求數列
,求數列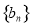 中的最大值.
中的最大值.
⑴見解析;⑵Sn= (n-1)·2n+1+2;⑶最大值為b1=0.5.
【解析】
試題分析:⑴利用等差數列的定義,研究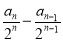 為定值;
為定值;
⑵由⑴進一步得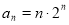 ,利用“錯位相減法”求和.
,利用“錯位相減法”求和.
根據Sn=1·21+2·22+3·23+ +(n-1)·2n-1+n·2n
2Sn=1·22+2·23+3·23+ +(n-1)·2n+n·2n+1
兩式相減得:-Sn=21+22+23+ +2n-n·2n+1 =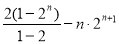
⑶由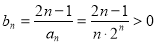
研究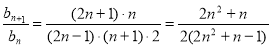 ,得到
,得到 推出{bn}為遞減數列
推出{bn}為遞減數列
數列{bn}中的最大值為b1.
試題解析:⑴∵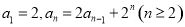
∴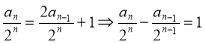
∴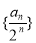 為等差數列,首項為
為等差數列,首項為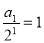 ,公差d=1(4分)
,公差d=1(4分)
⑵由⑴得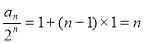 ∴
∴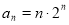 (6分)
(6分)
∴Sn=1·21+2·22+3·23+ +(n-1)·2n-1+n·2n
2Sn=1·22+2·23+3·23+ +(n-1)·2n+n·2n+1
兩式相減得:-Sn=21+22+23+ +2n-n·2n+1
=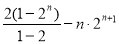
∴Sn=2-2n+1+n·2n+1=(n-1)·2n+1+2 (10分)
⑶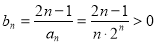
∴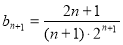 ∴
∴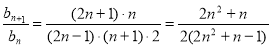 (12分)
(12分)
又∵2(2n2+n-1)-(2n2+n)=2n2+n-2
當n≥1時,2n2+n-2>0 ∴2(2n2+n-1)>2n2+n>0
∴ 即bn+1<bn
即bn+1<bn
∴{bn}為遞減數列 (14分)
數列{bn}中的最大值為b1=0.5
考點:等差數列,等比數列的求和,“錯位相減法”.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:高中數學 來源:2013-2014學年天津市高三5月理科數學試卷(解析版) 題型:選擇題
直線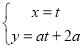 (t為參數)與曲線
(t為參數)與曲線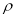 =1的位置關系是( )
=1的位置關系是( )
A.相離 B.相交 C.相切 D.不確定
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市高三5月文科數學試卷(解析版) 題型:填空題
某校有教師200人,男學生1200人,女學生1000人,現用分層抽樣的方法從所有教師中抽取一個容量為n的樣本;已知從女學生中抽取的人數為80人,則n的值為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市高三5月文科數學試卷(解析版) 題型:選擇題
若把函數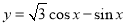 的圖象向右平移m個單位(m>0)后,所得到的圖象關于
的圖象向右平移m個單位(m>0)后,所得到的圖象關于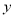 軸對稱,則m的最小值是( )
軸對稱,則m的最小值是( )
A.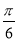 B.
B.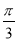 C.
C.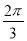 D.
D.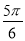
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市高考5月模擬理科數學試卷(解析版) 題型:選擇題
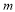 、
、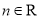 ,
,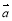 、
、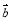 、
、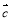 是共起點的向量,
是共起點的向量,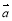 、
、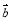 不共線,
不共線,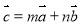 ,則
,則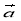 、
、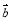 、
、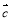 的終點共線的充分必要條件是( )
的終點共線的充分必要條件是( )
A.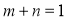 B.
B.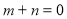 C.
C.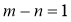 D.
D.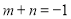
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市紅橋區高三第一次模擬考試文科數學試卷(解析版) 題型:填空題
如圖,AB是半圓O直徑,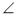 BAC=30o。BC為半圓的切線,且BC=4
BAC=30o。BC為半圓的切線,且BC=4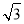 ,則點O到AC的距離OD= .
,則點O到AC的距離OD= .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com