
【題目】![]() 年
年![]() 月,電影《毒液》在中國上映,為了了解江西觀眾的滿意度,某影院隨機調查了本市觀看影片的觀眾,現從調查人群中隨機抽取部分觀眾.并用如圖所示的表格記錄了他們的滿意度分數(
月,電影《毒液》在中國上映,為了了解江西觀眾的滿意度,某影院隨機調查了本市觀看影片的觀眾,現從調查人群中隨機抽取部分觀眾.并用如圖所示的表格記錄了他們的滿意度分數(![]() 分制),若分數不低于
分制),若分數不低于![]() 分,則稱該觀眾為“滿意觀眾”,請根據下面尚未完成并有局部污損的頻率分布表(如圖所示),解決下列問題.
分,則稱該觀眾為“滿意觀眾”,請根據下面尚未完成并有局部污損的頻率分布表(如圖所示),解決下列問題.
組別 | 分組 | 頻數 | 頻率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合計 |
|
|
(1)寫出![]() 、
、![]() 的值;
的值;
(2)畫出頻率分布直方圖,估算中位數;
(3)在選取的樣本中,從滿意觀眾中隨機抽取![]() 名觀眾領取獎品,求所抽取的
名觀眾領取獎品,求所抽取的![]() 名觀眾中至少有
名觀眾中至少有![]() 名觀眾來自第
名觀眾來自第![]() 組的概率.
組的概率.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出樣本總容量![]() 的值,并計算出第
的值,并計算出第![]() 組的頻數,可求出
組的頻數,可求出![]() 的值,根據第
的值,根據第![]() 組的頻數和樣本總容量可計算出
組的頻數和樣本總容量可計算出![]() 的值;
的值;
(2)根據頻率分布表作出頻率分布直方圖,利用中位線左、右兩邊矩形面積和均為![]() 計算出中位數的值;
計算出中位數的值;
(3)設第![]() 組的
組的![]() 人記為
人記為![]() 、
、![]() 、
、![]() 、
、![]() ,第
,第![]() 組的
組的![]() 人記為
人記為![]() 、
、![]() ,利用列舉法列舉出所有的基本事件,并確定出事件“所抽取的
,利用列舉法列舉出所有的基本事件,并確定出事件“所抽取的![]() 名觀眾中至少有
名觀眾中至少有![]() 名觀眾來自第
名觀眾來自第![]() 組”所包含的基本事件數,利用古典概型的概率公式可計算出所求事件的概率.
組”所包含的基本事件數,利用古典概型的概率公式可計算出所求事件的概率.
(1)設樣本總容量為![]() ,由
,由![]() ,解得
,解得![]() ,
,![]() ,
,
設第![]() 組的頻數為
組的頻數為![]() ,則
,則![]() ,
,![]() ;
;
(2)頻率分布直方圖如下圖所示:

設中位數為![]() ,前兩組的頻率之和為
,前兩組的頻率之和為![]() ,
,
前三組的頻率之和為![]() ,則
,則![]() ,解得
,解得![]() ,
,
所以,中位數為![]() ;
;
(3)設第![]() 組的
組的![]() 人記為
人記為![]() 、
、![]() 、
、![]() 、
、![]() ,第
,第![]() 組的
組的![]() 人記為
人記為![]() 、
、![]() ,
,
則抽取![]() 人的基本事件為:
人的基本事件為:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 種,
種,
事件“所抽取的![]() 名觀眾中至少有
名觀眾中至少有![]() 名觀眾來自第
名觀眾來自第![]() 組”包含的基本事件為:
組”包含的基本事件為:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 個,
個,
因此,所抽取的![]() 名觀眾中至少有
名觀眾中至少有![]() 名觀眾來自第
名觀眾來自第![]() 組的概率為
組的概率為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的公差
的公差![]() ,數列
,數列![]() 滿足
滿足![]() ,集合
,集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() ,求
,求![]() 使得集合
使得集合![]() 恰好有兩個元素;
恰好有兩個元素;
(3)若集合![]() 恰好有三個元素:
恰好有三個元素:![]() ,
,![]() 是不超過7的正整數,求
是不超過7的正整數,求![]() 的所有可能的值.
的所有可能的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
如圖,長方體ABCD–A1B1C1D1的底面ABCD是正方形,點E在棱AA1上,BE⊥EC1.
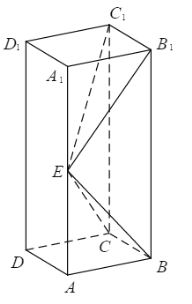
(1)證明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知二次函數![]() (
(![]() 、
、![]() 、
、![]() 均為實常數,
均為實常數,![]() )的最小值是0,函數
)的最小值是0,函數![]() 的零點是
的零點是![]() 和
和![]() ,函數
,函數![]() 滿足
滿足![]() ,其中
,其中![]() ,為常數.
,為常數.
(1)已知實數![]() 、
、![]() 滿足、
滿足、![]() ,且
,且![]() ,試比較
,試比較![]() 與
與![]() 的大小關系,并說明理由;
的大小關系,并說明理由;
(2)求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com