
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
分析 根據P是△ABC所在平面內一點,$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow 0$,得點P是△ABC的重心.再根據幾何概型公式,將△PBC的面積與△ABC的面積相除可得本題的答案.
解答 解:∵P是△ABC所在平面內一點,$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow 0$,
∴P是△ABC的重心,
∴點P到BC的距離等于A到BC的距離的$\frac{1}{3}$.
∴S△PBC=$\frac{1}{3}$S△ABC,
將一粒黃豆隨機撒在△ABC內,黃豆落在△PBC內的概率為P=$\frac{1}{3}$.
故選B.
點評 本題考查的知識點是幾何概型概率計算公式,計算出滿足條件和所有基本事件對應的幾何量,是解答的關鍵,難度中檔.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
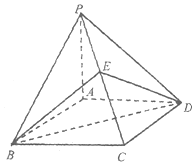 如圖,已知四棱錐P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直線PB和平面ABCD所成的角為45°,E為PC的中點.
如圖,已知四棱錐P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直線PB和平面ABCD所成的角為45°,E為PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $±\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (7,12) | B. | (12,15) | C. | (12,16) | D. | (15,16) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=ln(x-2) | B. | y=-$\sqrt{x}$ | C. | y=x2 | D. | y=$\frac{1}{x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知拋物線x2=4y,圓C:x2+(y-2)2=4,點M(x0,y0),(x0>0,y0>4)為拋物線上的動點,過點M的圓C的兩切線,設其斜率分別為k1,k2
已知拋物線x2=4y,圓C:x2+(y-2)2=4,點M(x0,y0),(x0>0,y0>4)為拋物線上的動點,過點M的圓C的兩切線,設其斜率分別為k1,k2查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com