Question

【題目】如圖，已知四棱錐中，底面為菱形，且， 是邊長為的正三角形，且平面平面，點是的中點.

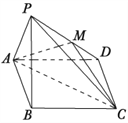
（1）證明： 平面；

（2）求三棱錐的體積.

Answer 1

【答案】（1）見解析（2）

【解析】試題分析：（1）連結交于，連結，由中位線定理可得，根據線面平行的判定定理可得平面；（2）取中點，連結，則平面，由，即可求出三棱錐的體積.

試題解析：（Ⅰ）連結交于，連結，

因為為菱形， ，所以，

由直線不在平面內， 平面，

所以平面.

（Ⅱ）取的中點，連接，則，且.

因為平面平面，所以平面.

所以，

又是中點，所以.

所以 .

【方法點晴】本題主要考查線面平行的判定定理、面面垂直的性質、線面垂直的判定、利用等積變換求三棱錐體積，屬于難題.證明線面平行的常用方法：①利用線面平行的判定定理，使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線，可利用幾何體的特征，合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質，即兩平面平行，在其中一平面內的直線平行于另一平面. 本題（1）是就是利用方法①證明的.